
Maintain variance

diffusion 모델은 분산을 1로 일정하게 유지
Var(xₜ) = Var(√(1-βₜ)xₜ₋₁) + βₜ
Var(xₜ) = (1-βₜ)Var(xₜ₋₁) + βₜ
Var(xₜ₋₁)는 1일 것으로 예상할 수 있으므로 Var(xₜ)도 1
즉, 디퓨전 과정 전반에 걸쳐 이미지의 '에너지'를 일정하게 유지하면서 점진적으로 원본 정보를 노이즈로 대체한다고 볼 수 있음
Loss Term
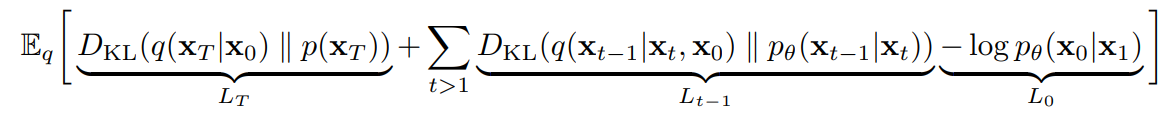
L_T는 최종 노이즈 분포를 표준 정규 분포와 유사하게 만드는 항
L_t-1은 시간 스텝에서의 KL 발산의 합으로, 실제 역과정 분포와 모델이 학습하는 역과정 분포를 유사하게 만드는 항
L0는 모델의 예측이 실제 데이터와 얼마나 일치하는지를 측정하여 최종 결과의 품질을 향상시키는 항
Conditional mean

ε_θ(x_t, t) 는 현재 이미지 x_t에 포함된 노이즈에 대한 추정
μ_θ(x_t, t) 는 이전 단계(t-1)로 이동할 때의 조건부 분포의 평균으로, 노이즈가 제거된 이전 단계 (t-1) 이미지의 추정치
즉, 현재 이미지 x_t에 포함된 노이즈에 대한 추정을 통해, 노이즈가 제거된 이전 단계 (t-1) 이미지의 추정치를 얻을 수 있음
Questions
reverse denoising process에서 초기에는 어떤 content를 만들지 결정되고 (low frequency 정보 생성), 후반에는 세부적인 부분을 형성 (high frequency 정보 생성)
Diffusion 모델의 U-Net에 시간 단계 t를 입력으로 넣는 이유?
-> t를 입력으로 받음으로써, 모델은 현재 이미지의 노이즈 수준을 인식 가능
-> 하나의 U-Net으로 모든 시간 단계를 처리할 수 있음
t를 단순히 정수로 입력하지 않고, Positional encoding을 사용하는 이유?
-> 모델이 시간 단계 간의 관계를 잘 학습하게 하기 위해 (디퓨전 과정의 초기와 후기 단계는 매우 다른 특성을 가짐)
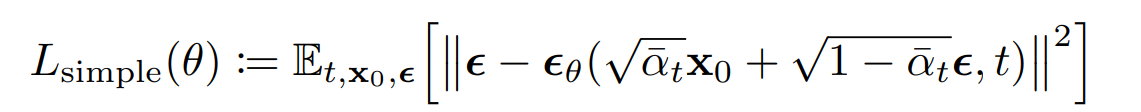
L_t-1항만 사용하는 이유?
-> L_T는 일반적으로 상수에 가깝거나 무시할 만한 크기
-> L_0는 계산이 복잡하고, 실제로 최적화하기 어려울 수 있음 (실제 이미지는 매우 복잡한 분포를 가지므로)
