Geometric transformation(기하학적 변환)은 Coordinate transformation(좌표 변환)과 Intensity interpolation(강도 보간)으로 구성된다.
좌표 변환(Coordinate transformation)은 입력 이미지의 픽셀이 출력 이미지에서 어디에 위치할지를 결정하는 과정이다. 이는 이미지의 회전, 이동, 크기 조절, 기울임 등과 같은 공간적 변형을 포함한다.
강도 보간(Intensity interpolation)은 변환된 좌표에서 픽셀의 실제 값을 결정하는 과정이다. 변환된 좌표가 정수가 아닌 실수 값을 가질 수 있으므로, 주변 픽셀들의 값을 이용하여 새로운 픽셀 값을 계산해야 한다. 이때 nearest neighbor, bilinear, bicubic 등의 보간 방법이 사용된다.
이 두 과정이 순차적으로 수행되어 최종적으로 변환된 이미지가 생성된다. 예를 들어 이미지를 45도 회전시키는 경우, 먼저 각 픽셀의 새로운 좌표를 계산하고(좌표 변환), 그 다음 계산된 좌표에서의 픽셀 값을 결정(강도 보간)하게 된다.
Translation
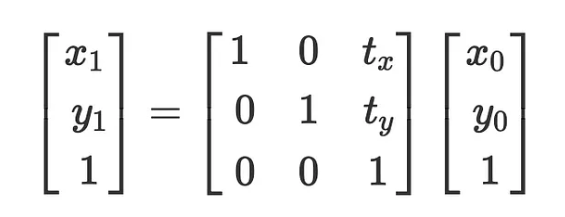
Rotation

Scaling
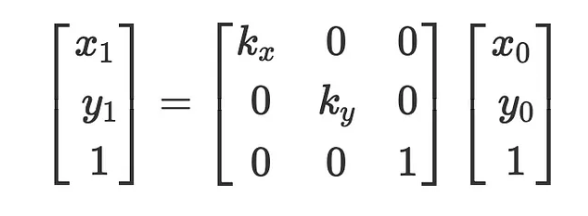
Shear

Affine
Affine 변환은 2차원 평면상에서 이루어지는 선형 변환이다. 가장 큰 특징은 평행선이 변환 후에도 평행을 유지한다는 점이다. 직선은 항상 직선으로 변환되며, 변환 전 한 직선 위에 있던 점들은 변환 후에도 여전히 한 직선 위에 존재한다. 하지만 거리와 각도는 보존되지 않을 수 있어, 이미지가 늘어나거나 기울어질 수 있다.
Affine 변환은 6개의 매개변수로 표현할 수 있으며, 이는 2x3 행렬로 나타낼 수 있다. 변환 행렬을 계산하기 위해서는 3개의 대응점만 있으면 충분한데, 이는 각 점이 x, y 좌표를 가지고 있어 총 6개의 방정식을 만들 수 있기 때문이다.
Perspective
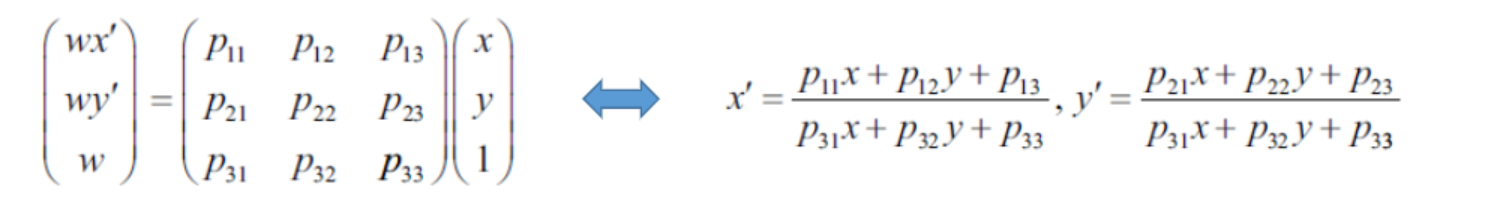
Perspective 변환은 3차원 공간에서의 원근감을 표현할 수 있는 더 복잡한 변환이다. 이 변환에서는 평행선이 반드시 평행을 유지하지 않으며, 원근감으로 인해 멀리 있는 물체가 작게 보이는 효과를 표현할 수 있다. 변환 과정에서 w로 나누는 단계가 포함되어 있어 비선형 변환이 되며, 이로 인해 직선성만 보존된다.
Perspective 변환은 8개의 파라미터로 표현되며, 이를 계산하기 위해서는 4개의 대응점이 필요하다. 이는 각 점이 제공하는 2개의 방정식을 통해 8개의 미지수를 풀 수 있기 때문이다.
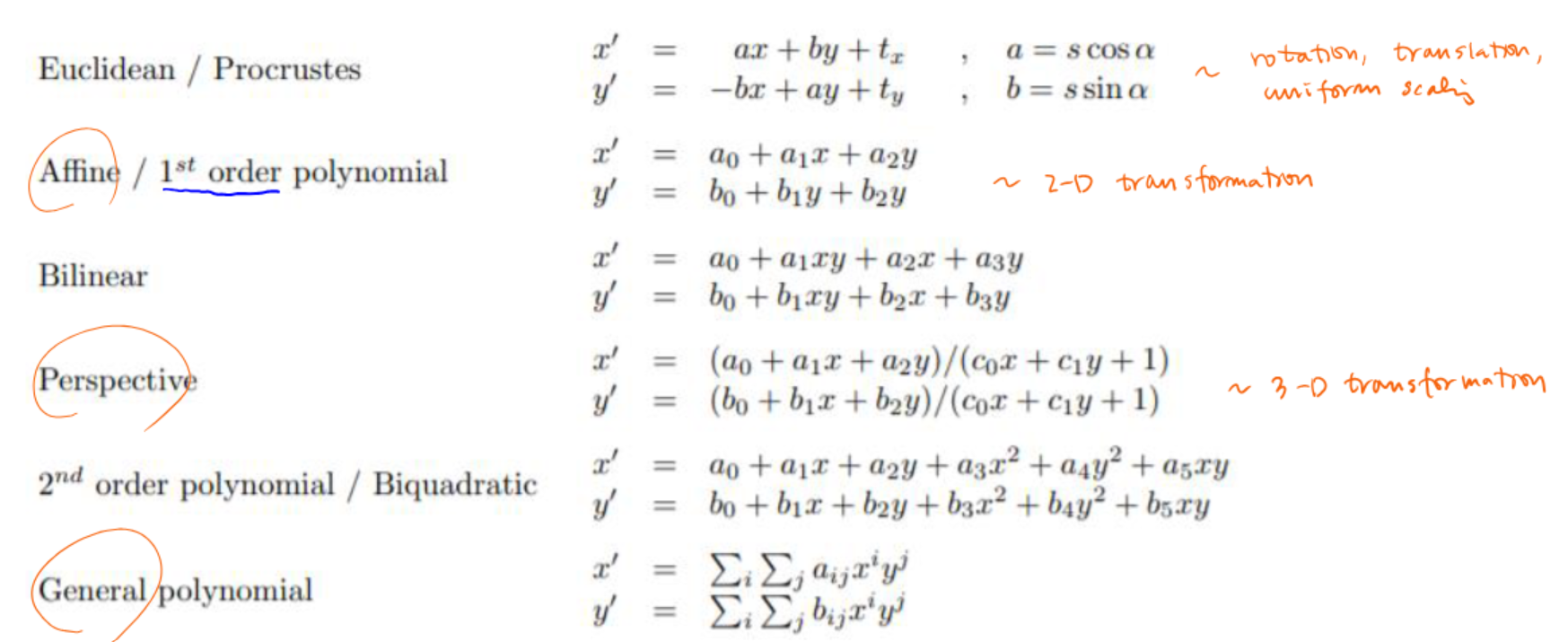
두 변환의 가장 큰 차이점은 적용 가능한 상황에 있다. Affine 변환은 2D 평면상의 단순한 변형에 적합하며, 평행성이 유지되어야 하는 경우에 사용된다. 반면 Perspective 변환은 3D 공간의 투영을 표현해야 하는 경우, 예를 들어 건물을 비스듬히 찍은 사진을 정면에서 본 것처럼 보정하거나, 문서를 스캔한 이미지를 바로 잡는 등의 작업에 적합하다.
Forward Mapping (정방향 매핑)
Forward Mapping(정방향 매핑)은 원본 이미지의 픽셀들을 하나씩 변환하여 새로운 위치로 이동시키는 방식이다. 원본 이미지의 각 픽셀 좌표 (x,y)에 변환 함수 T를 적용하여 출력 이미지의 좌표 (x',y')를 계산한다.
하지만 Forward Mapping은 몇 가지 중요한 문제점을 가지고 있다. 변환 후 일부 픽셀들 사이에 빈 공간(holes)이 생길 수 있으며, 여러 개의 원본 픽셀이 동일한 출력 위치에 매핑되어 중복(overlaps)이 발생할 수 있다. 또한 안티앨리어싱 처리가 어려워 이미지 품질이 저하될 수 있다.
Inverse Mapping (역방향 매핑)
Inverse Mapping(역방향 매핑)은 Forward Mapping의 문제점들을 해결하기 위한 대안적인 방법이다. 이 방식은 출력 이미지의 각 픽셀 위치에서 시작하여 역변환을 통해 원본 이미지의 해당 위치를 찾는다. 구체적으로, 출력 이미지의 각 픽셀 (x',y')에 대해 역변환 T^(-1)을 적용하여 원본 이미지의 좌표 (x,y)를 계산하고, 그 위치에서 보간법을 사용하여 픽셀 값을 결정한다.
Inverse Mapping의 장점은 출력 이미지의 모든 픽셀이 정확히 한 번씩 계산되므로 홀이나 중복이 발생하지 않는다는 것이다. 또한 보간 과정에서 안티앨리어싱을 자연스럽게 적용할 수 있어 더 높은 품질의 결과물을 얻을 수 있다.
Homogeneous Coordinates (동차좌표계)
동차좌표계(Homogeneous Coordinates)는 2차원의 점을 3차원 벡터로 표현하는 좌표계이다. 이는 2차원 좌표를 나타내는 방식이 3차원에서 무수히 많이 존재할 수 있음을 의미한다.
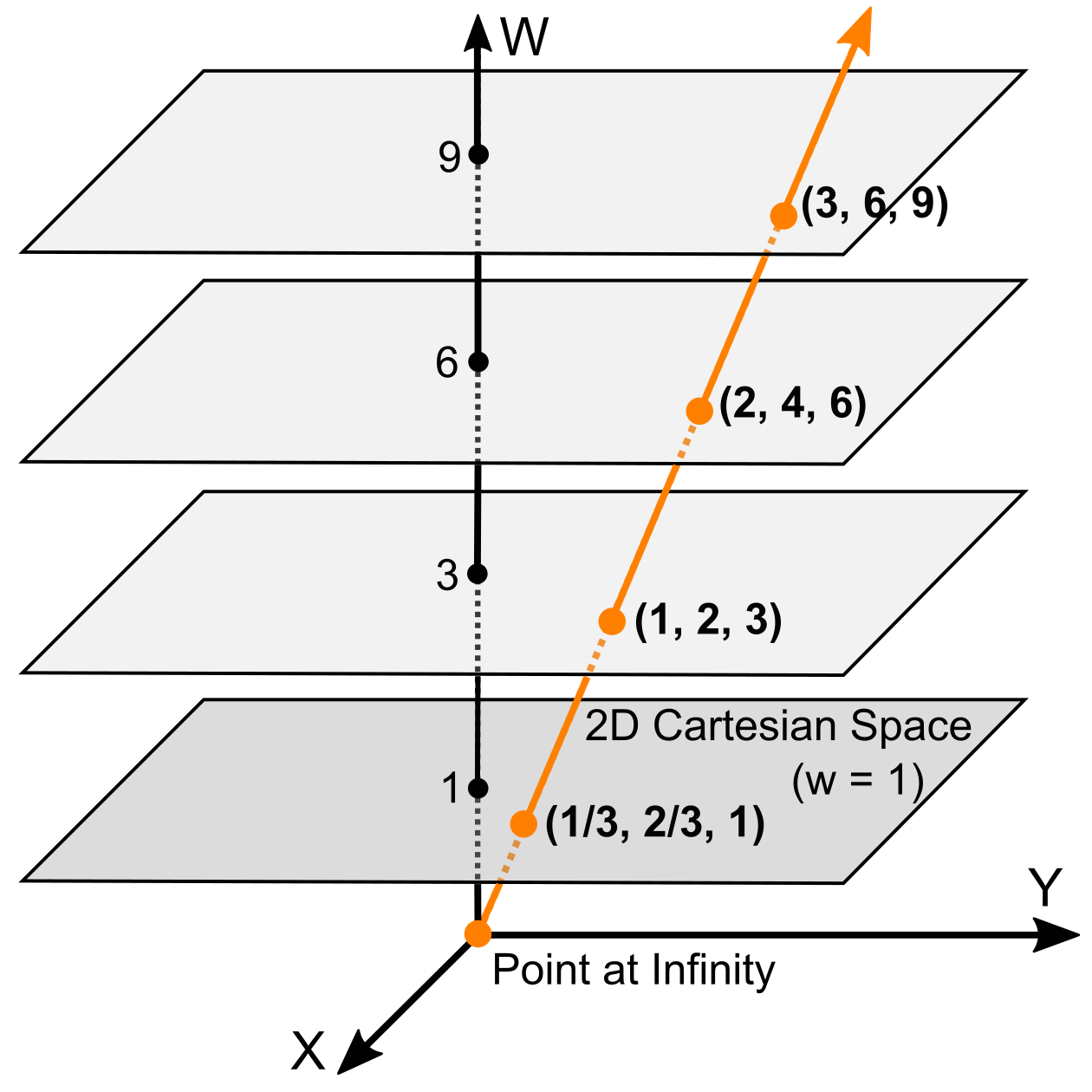
동차좌표계에서는 2차원의 점 (x,y)를 3차원 벡터 (x,y,w)로 표현한다. 실제 좌표는 w로 나눈 (x/w, y/w)가 된다. 따라서 하나의 2차원 점을 표현하는 방법이 무한히 많아진다. 예를 들어, (2,3,1), (4,6,2), (6,9,3)은 모두 2차원 평면상의 같은 점 (2,3)을 나타낸다.
동차좌표계의 주요 장점은 다음과 같다. 첫째, 여러 개의 변환을 순차적으로 적용할 때, 이를 하나의 행렬로 표현할 수 있다. 둘째, 평행이동을 포함한 모든 종류의 변환을 선형 변환으로 표현할 수 있다. 이는 계산을 단순화하고 일관된 방식으로 처리할 수 있게 해준다. 셋째, Perspective 변환과 같은 복잡한 3차원 투영을 표현할 수 있다.
파노라마 이미지 생성
파노라마 이미지 생성은 여러 장의 이미지를 하나의 넓은 시야각 이미지로 결합하는 과정이다. 이는 다음과 같은 주요 단계를 거쳐 이루어진다.
- 특징점 검출 및 매칭 단계에서는 SIFT나 SURF와 같은 알고리즘을 사용하여 각 이미지에서 특징점을 찾고, 이미지들의 겹치는 영역에서 대응되는 점들을 매칭한다.
- 변환 행렬 추정 단계에서는 RANSAC 알고리즘을 사용하여 호모그래피 행렬을 계산한다. 이 과정에서 잘못 매칭된 점들(이상치)을 제거하여 정확한 변환 행렬을 얻는다.
- 이미지 워핑 단계에서는 앞서 계산된 변환 행렬을 사용하여 이미지들을 변형한다. 이때 역방향 매핑 방식을 사용하여 이미지를 변환한다.
- 블렌딩 단계에서는 이미지들이 겹치는 영역에서 자연스러운 전환이 이루어지도록 처리한다. Feathering(가중치 평균), Multi-band blending(주파수 영역별 블렌딩), Graph-cut(최적의 이음새 찾기) 등 다양한 블렌딩 기법이 사용될 수 있다.
이미지 간의 Seam(이음새) 처리는 특히 중요하다. 이는 기하학적 정렬을 최적화하고, 색상과 밝기를 보정하며, 적응적 블렌딩 가중치를 적용하고, 로컬 정렬 기법을 사용하는 등의 방법으로 이루어진다. 이러한 세심한 처리를 통해 자연스러운 파노라마 이미지를 얻을 수 있다.
Image Registration
이미지 등록을 위해 일반적으로 다음 단계를 거친다:
- 특징 추출(Feature Extraction):
- 입력 이미지와 참조 이미지에서 특징점을 추출한다. 특징점은 일반적으로 코너, 에지, 혹은 중요한 패턴 등을 포함함
- 예: SIFT (Scale-Invariant Feature Transform), SURF (Speeded-Up Robust Features), Harris corners 등의 알고리즘이 사용됨
- 특징 매칭(Feature Matching):
- 두 이미지 간의 특징점을 매칭한다. 이 과정에서 거리 기반 매칭이나 최근접 이웃 매칭 방법을 사용할 수 있음
- 매칭된 특징점을 통해 두 이미지 간의 대응 관계를 파악
- 변환 행렬 계산(Transformation Matrix Calculation):
- 매칭된 특징점을 기반으로 변환 행렬을 추정한다. 변환 행렬은 이미지의 회전, 이동, 스케일링, 왜곡 등을 설명할 수 있음
- 예: RANSAC (Random Sample Consensus) 알고리즘을 사용하여 최적의 변환 행렬을 추정
- 이미지 변환(Image Transformation):
- 추정된 변환 행렬을 사용하여 입력 이미지를 기하학적으로 변환한다. 이 과정을 통해 입력 이미지를 참조 이미지와 정렬시킴
- OpenCV의 warpPerspective 함수 등을 사용할 수 있음
- 밝기 보간(Intensity Interpolation):
- 변환된 좌표에서 픽셀 값을 보간하여 최종 이미지를 생성함
2차원 변환에서는 3개의 점만 있으면 전체 변환을 결정할 수 있다. 이는 3점이 변환에 필요한 모든 정보를 포함하고 있기 때문에, 네 번째 점은 이미 결정된 변환에 의해 자동으로 정해진다.
하지만 실제 응용에서는 사람이 직접 대응점들을 일일이 선택하는 것이 현실적으로 불가능하다. 따라서 컴퓨터 비전 알고리즘을 통해 자동으로 특징점들을 검출하고 매칭하는 방법을 사용한다.
이 과정에서 자동으로 검출된 특징점들 중에는 잘못 매칭된 점들(outlier)이 포함될 수 있다. 따라서 RANSAC과 같은 알고리즘을 사용하여 이러한 outlier들을 제거하고, 정확하게 매칭된 점들(inlier)만을 선별하는 과정이 필요하다. 이렇게 선별된 inlier들을 사용하여 최종적인 변환 행렬을 계산하게 된다.
RANSAC
RANSAC (Random Sample Consensus) 알고리즘은 주어진 데이터에서 이상점(outliers)과 내재점(inliers)을 구별하여 모델을 추정하는 방법이다. 이는 다음과 같은 단계로 진행된다.
- 랜덤 샘플링: 전체 데이터셋에서 n개의 데이터 포인트를 무작위로 선택한다. 이때 선택되는 포인트 수는 추정하고자 하는 모델에 필요한 최소한의 개수이다.
- 모델 적합(Model Fitting): 선택된 랜덤 샘플 데이터를 사용하여 모델을 fitting한다. 이는 선택된 포인트들을 통해 가설적인 모델을 생성하는 과정이다.
- 오차 계산 및 분류: fitting된 모델과 전체 데이터 사이의 오차를 계산한다. 이 오차를 기준으로 각 데이터 포인트가 inlier인지 outlier인지 판단한다.
- 모델 재추정: 확인된 inlier 데이터들을 사용하여 모델을 다시 추정한다. 이때 가장 많은 consensus(동의)를 얻은 모델을 선택한다.
- 종료 조건 확인: 현재 모델이 설정된 목표치(inlier 개수 또는 비율)를 달성했는지 확인한다. 목표를 달성했다면 반복을 종료하고, 그렇지 않다면 1단계로 돌아가 과정을 반복한다.
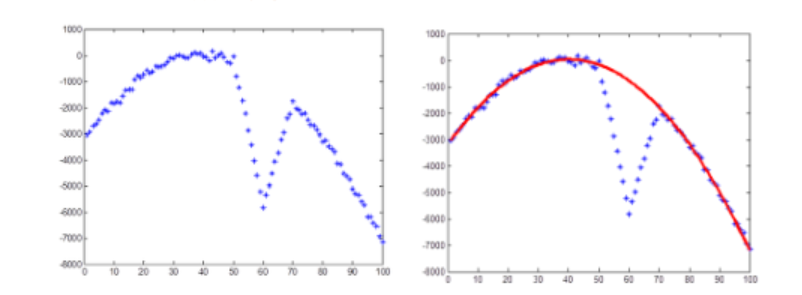
예를 들어, 2차 함수를 fitting하는 경우를 보면, 무작위로 3개의 점을 선택하여 2차 함수를 도출하고, 이 함수와 얼마나 많은 데이터 포인트가 일치하는지 확인한다. 이 과정을 여러 번 반복하면서 가장 많은 데이터 포인트와 일치하는 곡선을 찾아내는 것이다.
이미지의 시점 변환을 위한 homography matrix의 크기는 차원에 따라 다르게 결정된다.
2D 이미지 변환의 경우 3x3 크기의 homography matrix가 필요하다. 이는 2차원 평면상의 점을 동차좌표로 표현할 때 3차원 벡터 (x,y,w)를 사용하기 때문이다. 따라서 한 점에서 다른 점으로의 변환을 표현하기 위해서는 3x3 행렬이 필요하다.
3D 이미지 변환의 경우 4x4 크기의 homography matrix가 필요하다. 3차원 공간상의 점을 동차좌표로 표현할 때는 4차원 벡터 (x,y,z,w)를 사용하기 때문이다. 따라서 3차원 공간에서의 변환을 표현하기 위해서는 4x4 행렬이 필요하다.
이러한 차이는 동차좌표계에서 각 차원의 점을 표현하는 데 필요한 좌표의 수가 다르기 때문에 발생한다. 좌표의 수가 하나 더 많은 이유는 perspective 변환과 같은 투영 변환을 선형 변환으로 표현하기 위해서이다.
'학교공부 > 영상처리' 카테고리의 다른 글
| [영상처리] Image Resizing (0) | 2024.11.15 |
|---|
