[알고리즘] 백트래킹

백트래킹은 해를 찾는 도중에 '막히면' 되돌아가서 다시 해를 찾아가는 전략이다. 모든 가능한 경우의 수를 전부 살펴보는 브루트 포스(Brute Force) 방식과 달리, 백트래킹은 현재 상태에서 해가 될 가능성이 없다고 판단되면 더 이상 그 방향으로 탐색하지 않고 이전으로 돌아간다.

 

 

 

 

N-Queens 문제

---

N-Queens 문제는 N×N 체스판에 N개의 퀸을 서로 공격할 수 없도록 배치하는 문제이다.

 

알고리즘 구현:

 

c

void queens(index i) {
    index j;
    if(promising(i))
        if(i==n)
            cout << col[1] through col[n];
        else
            for(j=1; j<n; j++) {
                col[i+1] = j;
                queens(i+1);
            }
}

유망성 검사:

 

c

bool promising(index i) {
    index k;
    bool switch;
    
    k=1;
    switch = true;
    while(k<i && switch) {
        // 같은 열이거나 같은 대각선상에 있는지 확인
        if(col[i]==col[k] || abs(col[i]-col[k]) == i-k)
            switch = false;
        k++;
    }
    return switch;
}

 

 

 

유망성 검사에서는 두 가지를 확인한다:

1. 같은 열에 있는지 (col[i]==col[k])
2. 같은 대각선상에 있는지 (abs(col[i]-col[k]) == i-k)

 

위 그림에서는 8-Queens 문제를 해결하는 과정을 보여주고 있으며, 이미지 2는 N-Queens 문제의 코드 구현을 보여준다. 여기서 col[i]는 i번째 행에 있는 퀸의 열 위치를 나타낸다.

 

 

 

 

 

 

 

 

부분집합의 합 문제

---

이 문제는 n개의 양의 정수 집합에서 합이 특정 값 W가 되는 부분집합을 찾는 문제이다.

 

상태공간 트리 표현:

 

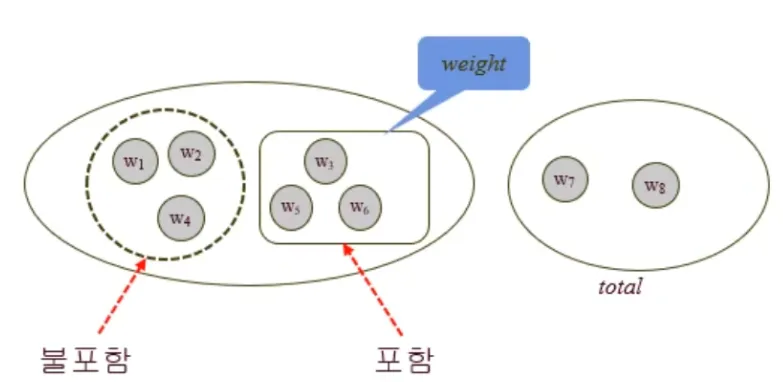
위 그림은 부분집합의 합 문제를 해결하기 위한 개념적 모델을 보여준다:

• weight: 현재까지 선택한 원소들의 무게 합
• total: 아직 고려하지 않은 모든 원소들의 무게 합
• 불필요한 탐색을 줄이기 위한 조건: weight + wi+1 > W 이거나 weight + total < W일 때는 더 이상 탐색하지 않는다.

 

 

알고리즘 구현:

 

c

void sum_of_subsets(index i, int weight, int total) {
    if(promising(i))
        if(weight == W)
            cout << include[1] through include[i];
        else {
            include[i+1]="yes";
            sum_of_subsets(i+1, weight+w[i+1], total-w[i+1]);
            include[i+1]="no";
            sum_of_subsets(i+1, weight, total-w[i+1]);
        }
}

 

유망성 검사:

 

c

bool promising(index i) {
    return (weight+total>=W) && (weight == W || weight+w[i+1]<=W);
}

 

 

 

위 그림의 예시에서는 n=4, W=13, w₁=3, w₂=4, w₃=5, w₄=6인 경우를 보여준다. 이 문제의 해는 {w₁, w₄} = {3, 6} 조합으로, 합이 정확히 13이 된다.

 

 

 

 

 

 

 

그래프 색칠하기 문제

m개의 색으로 n개의 정점을 갖는 무방향 그래프를 색칠하는 문제로, 인접한 정점은 서로 다른 색을 가져야 한다.

 

 

알고리즘 구현:

c

void m_coloring(index i) {
    int color;
    if(promising(i))
        if(i==n)
            cout << vcolor[1] through vcolor[n];
        else
            for(color=1; color<=m; color++) {
                vcolor[i+1] = color;
                m_coloring(i+1);
            }
}

 

 

유망성 검사:

c

bool promising(index i) {
    index j;
    bool switch;
    
    switch = true;
    j=1;
    while(j<i && switch) {
        if(W[i][j] && vcolor[i]==vcolor[j])  // W[i][j]: 연결표시, T or F
            switch = false;
        j++;
    }
    return switch;
}

 

 

 

위 그림은 그래프 색칠하기 문제의 구현을 보여준다. vcolor[i]는 노드 i의 색을 나타내며, W[i][j]는 노드 i와 j가 연결되어 있는지를 나타내는 인접 행렬이다.

 

 

그래프 색칠하기 문제에서 m개의 색과 n개의 정점이 있을 때, 상태공간 트리 상의 마디 총수는 기하급수적으로 증가한다: 1 + m + m² + ... + mⁿ = (m^(n+1) - 1) / (m - 1)