[자료구조] Binary Search Tree

오늘은 '이진 탐색 트리'에 대해서 공부해보았다.

 

우선 이진 탐색 트리에 대해 알기 전에 '트리'라는 개념을 먼저 살펴보자.

 

 

이진 트리(Binary Tree)

 

트리란 그래프의 일종으로, 노드들이 나뭇가지처럼 연결된 형태를 띄는 비선형 자료구조이다.

 

비선형 자료구조라는 것은 스택, 큐와 같이 하나의 자료 뒤에 하나의 자료가 연결되어 있는 선형 자료구조와 달리 하나의 자료 뒤에 여러 개의 자료가 연결될 수 있는 구조를 뜻한다.

 

 

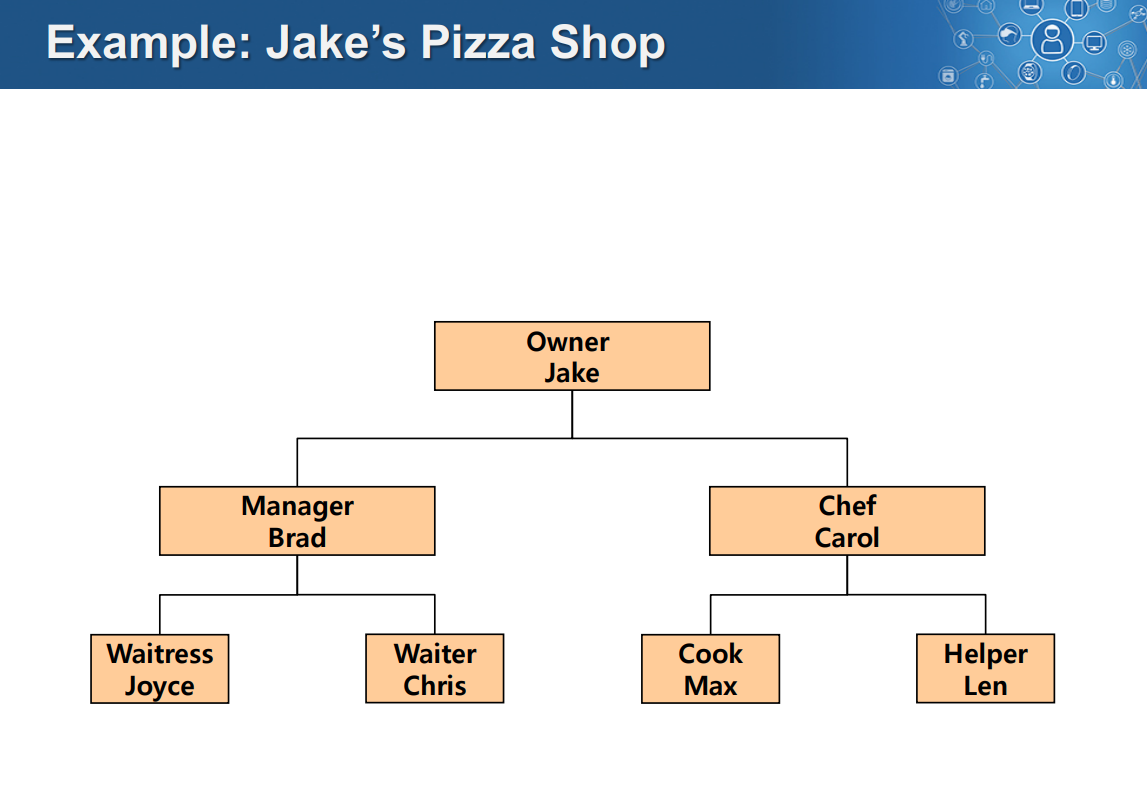
위 그림은 트리의 일종인 이진 트리의 예시 중 하나이다.

 

이진 트리는 자식 노드를 최대 두 개 가지는 트리를 뜻한다. 여기서 노드(node)란 위 그림에서 사각형 박스를 의미하며 일반적으로 데이터가 그 안에 담긴다. 그리고 이 노드들을 이어주는 선을 엣지(edge)라고 부른다. 어떤 노드가 A가 있을 때 그 노드의 아래 쪽에 연결되어 있는 노드 B를 노드 A의 '자식' 노드라고 하며 A는 B의 '부모' 노드라 부른다. 즉 이진 트리는 아래 쪽에 연결되어 있는 노드가 2개 이하인 트리를 뜻한다.

 

 

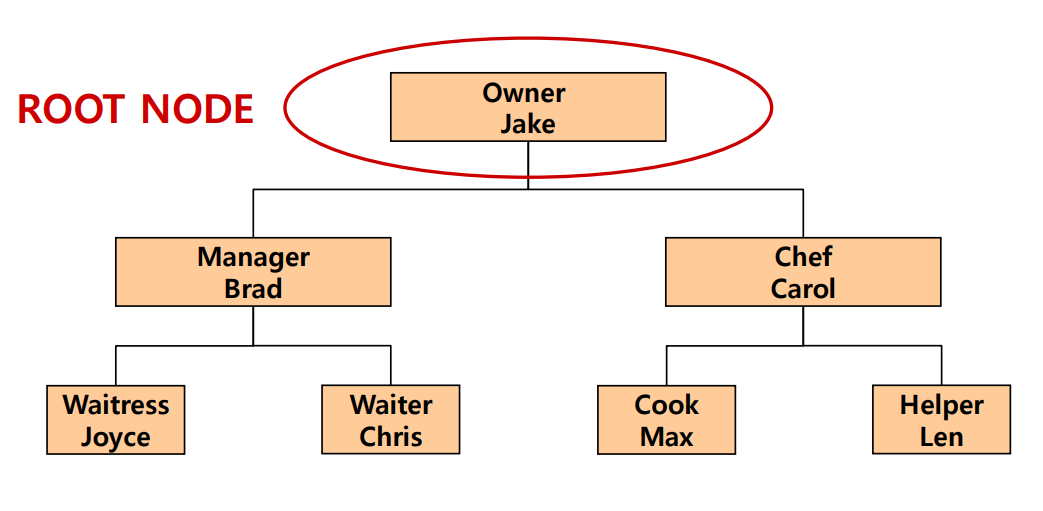
트리의 제일 위에 있는 노드, 부모 노드가 없는 노드를 '루트' 노드(root node)라 부른다. 반대로 트리의 제일 아래 있는 노드, 자식 노드가 없는 노드를 '잎새' 노드(leaf node)라 부른다. 

 

트리의 깊이를 보통 레벨로 표현하는데 루트 노드를 Level 0으로 하여 한 칸 씩 내려갈 때마다 레벨이 높아지는 식이다.

 

트리는 특정 노드를 기준으로 왼쪽과 오른쪽의 더 작은 트리들로 구성되어 있다고 볼 수 있는데 노드 A의 좌측에 연결된 트리를 A의 left subtree, 우측에 연결된 트리를 A의 right subtree라고 한다.

 

 

이진 탐색 트리(Binary Search Tree)

 

이번엔 이진 탐색 트리(Binary Search Tree)에 대해 살펴보자. BST는 아래와 특성을 만족하는 이진 트리이다.

 

1. 각 노드에는 고유한 데이터 값이 존재
2. 트리의 키 값은 '보다 큼'과 '보다 작음'을 사용하여 비교 가능
3. 트리에서 각 노드의 키 값은 오른쪽 하위 트리의 모든 키 값보다 작고 왼쪽 하위 트리의 모든 키 값보다 큼

쉽게 말해 BST는 각 노드의 데이터 값을 비교함으로써 노드의 추가, 제거, 탐색이 가능한 자료구조이며, 각 노드는 자신의 왼쪽 자식 노드보다는 크고 오른쪽 자식 노드보다는 작다는 특징을 가진다.

 

예를 들어 알파벳을 데이터 값으로 가지는 BST를 생각해보자.

 

첫번째로 루트 노드에 'J'가 들어있다.

다음으로 'E'를 BST에 추가한다고 하면 'E'는 'J'보다 작으므로 'J'의 왼쪽 자식이 된다.

다음으로 'F'를 추가해보자. 'F'는 'J'와 비교해 더 작으므로  'J'의 왼쪽 자식 노드가 되었어야 했으나 이미 'J'의 왼쪽 자식 노드 'E' 가 존재한다. 때문에 'F'는 'E'보다 크기 때문에 'E'의 오른쪽 자식 노드로 들어간다.

다음으로 'T'가 들어온다면 'T'는 'J'보다 크기 때문에 'J'의 오른쪽 자식 노드가 된다.

 

BST 구현

그럼 이제 이진 탐색 트리를 직접 구현해보자.

 

노드 구조체

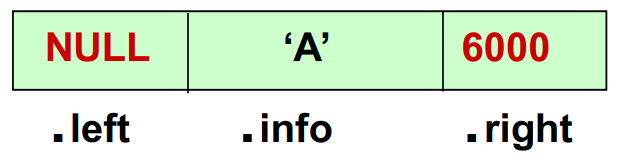
우선 이진 트리이기 때문에 한 개의 노드는 좌측 노드와 우측 노드를 가질 가능성이 있으므로 왼쪽 자식과 오른쪽 자식에 대한 포인터를 가지고 있어야 할 것이다. 물론 노드 본인의 데이터 또한 가지고 있어야 한다. 때문에 노드의 구조는

template< class ItemType >
struct TreeNode
{ 
ItemType info; // Data member
TreeNode<ItemType>* left; // Pointer to left child
TreeNode<ItemType>* right; // Pointer to right child
};

 

노드의 구조

 

BST 클래스

이진 탐색 트리의 클래스는 아래와 같이 구성된다.

template< class ItemType >
class TreeType
{
public:
	TreeType(); // constructor
	~TreeType(); // destructor
	TreeType(const TreeType& originalTree); // copy constructor
	void operator =(const TreeType& originalTree);
	void MakeEmpty();
	bool IsEmpty() const;
	bool IsFull() const;
	void ResetTree(OrderType order);
	int LengthIs() const;
	void RetrieveItem(ItemType& item, bool& found) const;
	void InsertItem(ItemType item);
	void DeleteItem(ItemType item);
	void GetNextItem (ItemType& item, OrderType order, bool& finished);
	void Print(std::ofstream& outFile) const;
private:
	TreeNode<ItemType>* root;
};

이제부터 BST 클래스를 구성하는 함수에 대해 하나씩 살펴보자.

 

 

 

IsFull() 함수

노드가 더 채워질 수 있는지 판단하는 IsFull() 함수는

template<class ItemType>
bool TreeType<ItemType> :: IsFull() const
// Returns true if there is no room for another item
// on the free store; false otherwise.
{
	TreeNode* location;
	try
    	{
		location= new TreeNode;
		delete location;
		return false;
	}
	catch(std::bad_alloc exception) 
	{
	return true;
	}
}

노드 하나를 동적할당한 후 삭제하여 노드가 추가될 수 있는지 확인하고 추가가 가능하면 false를, 메모리 공간이 부족하여 추가가 불가능하면 true를 반환한다.

 

 

IsEmpty() 함수

BST가 비었는지 확인하는 IsEmpty() 함수는

template< class ItemType>
bool TreeType<ItemType> :: IsEmpty() const
// Returns true if the tree is empty; false otherwise.
{
return root == NULL;
}

BST는 무조건 root부터 채워지므로 root가 NULL이라는 것은 트리가 비어있음을 뜻한다.

 

 

LengthIs() 함수

BST의 노드 개수를 새주는 함수

template< class ItemType > int CountNodes(TreeNode<ItemType>* tree);

template< class ItemType >
int TreeType<ItemType> :: LengthIs() const
// Calls recursive function CountNodes to count the
// nodes in the tree.
{
	return CountNodes(root);
}

template< class ItemType >
int CountNodes(TreeNode<ItemType>* tree)
// Post: returns the number of nodes in the tree.
{
	if (tree == NULL)
		return 0;
	else
		return CountNodes(tree->left) + CountNodes(tree->right) + 1;
}

재귀함수인 CountNodes 함수로 노드의 개수를 센 후 그 값을 반환한다. 

 

 

RetrieveItem 함수

template< class ItemType >
void TreeType<ItemType> :: RetrieveItem ( ItemType& item, bool& found )
{
	Retrieve ( root, item, found ) ;
}
template< class ItemType >
void Retrieve ( TreeNode<ItemType>* ptr, ItemType& item, bool& found)
{
	if ( ptr == NULL ) 
		found = false ;
	else if ( item < ptr->info ) // GO LEFT
		Retrieve( ptr->left , item, found ) ;
	else if ( item > ptr->info ) // GO RIGHT
		Retrieve( ptr->right , item, found ) ;
	else 
	{
		item = ptr->info ;
		found = true ;
	}
}

 

 

Insert() 함수

template< class ItemType >
void TreeType<ItemType> :: InsertItem ( ItemType item )
{
	Insert ( root, item ) ;
}

template< class ItemType >
void Insert ( TreeNode<ItemType>*& ptr, ItemType item )
{
	if ( ptr == NULL ) 
	{ 									// INSERT item HERE AS LEAF
		ptr = new TreeNode<ItemType> ;
		ptr->right = NULL ;
		ptr->left = NULL ;
		ptr->info = item ;
	}
	else if ( item < ptr->info ) // GO LEFT
		Insert( ptr->left , item ) ;
	else if ( item > ptr->info ) // GO RIGHT
		Insert( ptr->right , item ) ;
}

 

 

Delete() 함수

template< class ItemType > void Delete(TreeNode*& tree, ItemType item);

template< class ItemType >
void TreeType<ItemType>::DeleteItem(ItemType item)
// Calls the recursive function Delete to delete item from tree.
{
	Delete(root, item);
}

template< class ItemType >
void Delete(TreeNode*& tree, ItemType item)
// Deletes item from tree
// Post : item is not in tree
{
	if (item < tree->info)
		Delete(tree->left, item); // Look in left subtree.
	else if (item > tree ->info)
		Delete(tree->right, item); // Look in right subtree.
	else
		DeleteNode(tree); // Node found; call DeleteNode.
}

template< class ItemType > void GetPredecessor(TreeNode* tree, ItemType& data);

template< class ItemType >
void DeleteNode(TreeNode*& tree)
{
	ItemType data;
	TreeNode* tempPtr;
	tempPtr = tree;
	if(tree->left == NULL)
	{
		tree = tree->right;
		delete tempPtr;
	}
	else if (tree->right == NULL)
	{
		tree = tree->left;
		delete tempPtr;
	}
	else
	{	GetPredecessor(tree->left, data);
		tree->info = data;
		Delete(tree->left, data); //Delete predecessor node.
	}
}

template< class ItemType >
void GetPredecessor (TreeNode* tree, ItemType& data)
// Sets data to the info member of the rightmost
// node in tree.
{
	while(tree->right != NULL)
	tree = tree->right;
	data = tree->info;
}