[기계학습] 가중치 감쇠

Underfitting / Overfitting

머신러닝에서 underfitting과 overfitting은 모델이 데이터를 어떻게 학습하고 일반화하는지에 대한 중요한 개념이다.

• Underfitting: 이는 모델이 학습 데이터를 충분히 학습하지 못해, 데이터의 패턴을 제대로 파악하지 못하는 상황을 말한다. 이 경우, 모델은 학습 데이터에서도 낮은 성능을 보이며, 새로운 데이터에 대해서도 잘 예측하지 못한다. Underfitting은 주로 모델의 복잡성이 너무 낮아 발생하며, 이는 모델이 너무 단순하여(모델의 용량이 너무 작음) 데이터의 복잡성을 캡처할 수 없음을 의미한다.
• Overfitting: 반면에 overfitting은 모델이 학습 데이터를 너무 과도하게 학습하여, 특정 학습 데이터에만 과도하게 최적화된 상태를 말한다. 이 경우, 모델은 학습 데이터에서는 높은 성능을 보여주지만 새로운 데이터(검증 또는 테스트 세트)에 대해서는 낮은 성능을 보일 수 있다. Overfitting은 주로 모델의 복잡성이 너무 높거나, 충분한 양의 학습용 데이터가 제공되지 않았을 때 발생한다.

 

 

Overfitting의 해결책

Underfitting의 경우 학습 데이터가 어느 정도 충분하다면 비교적 쉽게 해결될 수 있지만 Overfitting의 경우 해결이 더 어렵다. 모델이 너무 복잡하고 파라미터가 많으면, 학습 데이터의 노이즈까지도 학습하게 될 가능성이 있다. 이 경우, 각 파라미터 계수들은 특정한 학습 데이터 샘플들에 의해 과도하게 커질 수 있다. 결과적으로 모델이 새로운 데이터를 잘 일반화하지 못하는 overfitting 상태를 초래한다. 이 경우 '규제' 기법을 사용해 문제를 해결할 수 있다.

 

 

 

 

 

Regularization(규제)

규제는 오래 전부터 수학과 통계학에서 연구해온 주제로써 모델 용량에 비해 데이터가 부족한 불량문제를 푸는데 사용되었다.

 

규제에는 보통 명시적 규제와 암시적 규제로 나눌 수 있다:

1. 명시적 규제: 가중치 감쇠나 드롭아웃처럼 목적함수나 신경망 구조를 직접 수정하는 방식
2. 암시적 규제: 조기 멈춤, 데이터 증대, 잡음 추가, 앙상블처럼 간접적으로 영향을 미치는 방식

 

 

 

가중치 감쇠

가중치 감쇠(weight decay)는 머신러닝 모델의 과적합을 방지하는 데 사용되는 정규화(regularization) 기법 중 하나이다. 가중치 감쇠는 모델의 학습 과정에서 가중치 파라미터가 너무 커지는 것을 방지함으로써, 모델이 학습 데이터에 과도하게 적합하는 것을 막는다.

 

가중치 감쇠를 적용하는 방법은 손실 함수(loss function)에 가중치에 따른 패널티 항(또는 규제 항)을 추가하는 것이다. 이 패널티 항은 전체 손실을 증가시키므로, 이를 최소화하기 위해 모델은 가능한 작은 가중치 값을 선택하게 된다.

 

이때 사용되는 규제항으로는 L1 Norm과 L2 Norm이 있다.

 

L1 Norm:

L1 Norm은 벡터의 각 요소의 절대값을 합한 것으로 가중치를 고정값만큼 줄인 후 업데이트 하는 것으로 볼 수 있다. 이 경우 0이 되는 가중치들이 발생하게 된다. 이를 선형회귀에 적용하면 특징 선택 효과를 얻을 수 있다.

 

 

L2 Norm:

L2 Norm은 벡터의 각 요소를 제곱한 후 합하고, 그 결과에 대해 제곱근을 취한 것이다. L2 규제는 가중치를 일정 비율로 줄인 후 업데이트하는 것으로 볼 수 있다. 즉 가중치의 감소율은 현재 가중치의 크기에 비례한다.

 

L2 Norm을 적용한 목적함수의 gradient를 0으로 두고 가중치를 구하면 다음과 같다.

 

 

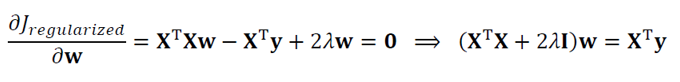
가중치 파라미터와 달리 편향 파라미터의 경우 규제를 적용하지 않는 경우가 많다. 가중치와 달리 편향은 입력 데이터와 직접 곱해지지 않는다. 따라서 편향 값이 커져도 모델의 복잡성이 크게 증가하지 않으며, 이로 인해 발생하는 과적합 위험도 상대적으로 낮다. Non-centered dataset에 규제를 적용할 경우 오히려 예측률이 떨어지기도 하기 때문에 편향 파라미터에는 규제를 적용하지 않는다.