암시적 규제의 기술: 조기 멈춤부터 데이터 증강까지
규제에는 두 얼굴이 있다. 하나는 직접적이고, 다른 하나는 간접적이다. 지난 시간 배운 가중치 감쇠나 구조 수정은 명시적 규제였다. 오늘은 그 반대편, 암시적 규제에 대해 이야기하려 한다. 결과적으로 규제 효과를 가져오지만, 직접 규제를 가하지 않는 방법들이다.
조기 멈춤: 가장 단순하면서도 효과적인
조기 멈춤(Early Stopping)은 구현이 매우 쉽다는 장점이 있다. 통찰은 단순하다. 학습이 진행될수록 훈련 오류는 계속 감소한다. 하지만 검증 오류는? 처음에는 감소하다가 어느 순간 다시 증가한다. 그 전환점이 바로 과적합이 시작되는 지점이다.
해결책은 명확하다. 검증 오류가 증가하기 직전에 학습을 멈추면 된다. 과적합이 일어나기 전의 모델을 얻는 것이다. 이론적으로는 완벽하다. 하지만 실전은 다르다.
현실의 복잡함
현실의 검증 오류는 부드럽게 증가하지 않는다. 샘플에 노이즈가 많아서 그래디언트가 오르락내리락한다. 떨어졌다 올라갔다를 반복한다. 만약 한 번 증가했다고 바로 멈춘다면? 뒤에 더 좋은 로컬 미니멈을 찾을 기회를 놓친다. 설익은 수렴이다.
기본 알고리즘은 이렇다. 난수로 초기 해를 설정한다. 최소 오류를 큰 값(1.0)으로 둔다. 매 iteration마다 θ_t에서 θ_(t+1)로 업데이트한다. 검증 오류를 비교한다. 증가했으면 멈춘다. 하지만 이것은 현실에서 전혀 작동하지 않는다.
참을성의 미덕
해결책은 "참을성(Patience)"이다. 검증 오류가 증가해도 바로 멈추지 않는다. 한 번 더 본다. 또 증가해도 참는다. P번까지 참는다. 이것이 참을성 인자다.
여기에 "세대 반복 인자(Q)"를 추가한다. 매 iteration마다 체크하지 않고, Q iteration마다 체크한다. 예를 들어 Q=10이면 1번째, 11번째, 21번째... 이렇게 듬성듬성 샘플링한다. Interval이 커서 학습을 더 길게 가져갈 수 있다.
알고리즘은 이렇게 작동한다. Q interval마다 검증 오류를 측정한다. 최저 오류보다 낮으면? 업데이트한다. 높거나 같으면? 참을성 카운터 j를 1 증가시킨다. j가 P에 도달하면? 더 이상 못 참고 종료한다.

참을성과 계산 자원의 균형
P와 Q를 어떻게 설정할까? 계산 자원이 충분하다면 P를 크게 한다. 더 오래 참으면서 최선의 지점을 찾는다. 자원이 부족하면? P와 Q를 줄여서 빠르게 조기 멈춤을 실행한다. 트레이드오프다.
중요한 점은 이것이 iteration이 아니라 "훈련 횟수"라는 것이다. 한 번 훈련에 10시간씩 걸릴 수 있다. Q 값이 처음에는 올라가다가, 안 좋은 hyperparameter로 계속 학습하면 정체한다. 좋은 것을 찾으면 다시 올라간다. 계단식으로 조금씩 더 좋은 Q를 찾아간다.
조기 멈춤은 신기한 방법이다. 과적합이 되기 전에 학습을 끝낸다. 단순하지만 강력하다.
데이터 증강: 최고의 해결책
과적합을 막는 가장 확실한 방법은 무엇일까? 큰 훈련 집합을 사용하는 것이다. 데이터가 많으면 모든 문제가 해결된다. 무한한 데이터가 있다면? 규제도, 조기 멈춤도 필요 없다. 모델을 키울 때마다 성능이 쭉쭉 올라간다.
간단한 예를 보자. 20개 샘플로 12차 다항식을 피팅하면 어떻게 될까? 뾰족뾰족한 과적합이 발생한다. 하지만 40개, 60개로 늘리면? 12차 다항식이어도 부드럽게 피팅된다. 데이터가 많은 것이 최고다.
자연어 처리의 역전
흥미로운 역사가 있다. 과거에는 컴퓨터 비전이 AI를 선도했다. 최신 기술이 비전에서 나오면 자연어 처리 연구자들이 가져다 썼다. 그런데 어느 순간 역전됐다. 지금은 자연어 처리가 리드하고 비전이 따라간다.
이유는 사람 수가 아니었다. 데이터 때문이었다. 하루를 돌아보자. 사진을 몇 장 찍는가? 카톡은 몇 번 보내는가? 사진은 안 찍는 날이 있어도 카톡을 안 보내는 사람은 없다. 텍스트 데이터가 압도적으로 많다.
ChatGPT가 자연어 처리에서 먼저 나온 것은 이상한 일이 아니다. 인터넷에 수없이 많은 글들. 그것이 학습 데이터가 됐다. 데이터가 많으면 좋은 모델을 만들 수 있다. 결국 데이터 싸움이다.
인위적 데이터 증강
데이터가 부족할 때 어떻게 할까? 인위적으로 확대한다. 데이터 증강(Data Augmentation)이다. 자연계에서 벌어지는 잠재적 변형을 프로그램으로 흉내낸다.
MNIST를 예로 들어보자. 숫자 1을 쓸 때 사람마다 다르다. 어떤 사람은 반듯하게, 어떤 사람은 기울여서, 어떤 사람은 45도로. 크게 쓰는 사람도 있고 작게 쓰는 사람도 있다. 중앙에 쓰기도 하고 왼쪽이나 오른쪽에 붙여 쓰기도 한다. 이 모든 것이 자연스럽게 발생할 수 있는 변형이다.

Affine 변환의 한계
Affine 변환으로 이를 시뮬레이션할 수 있다. 이동(왼쪽, 오른쪽, 위, 아래), 회전(5도, 10도, 45도), 크기 변화(작게, 크게). 하나의 샘플에서 거의 무한한 샘플을 만든다. 네트워크 입장에서는 데이터가 많아지니 과적합을 피할 수 있다.
하지만 한계가 있다. 첫째, 수작업이다. 이동을 몇 픽셀 할지, 회전을 90도까지 할지 180도까지 할지, 크기를 몇 배까지 할지. 인간이 정해야 한다. 둘째, 모든 부류가 같은 변형을 쓰면 문제가 생긴다. 6을 180도 회전하면? 9가 된다. 레이블은 여전히 6인데 이미지는 9다. 네트워크는 혼란에 빠진다. 하나의 노이즈 때문에 성능이 급락한다.
AlexNet의 영리한 전략
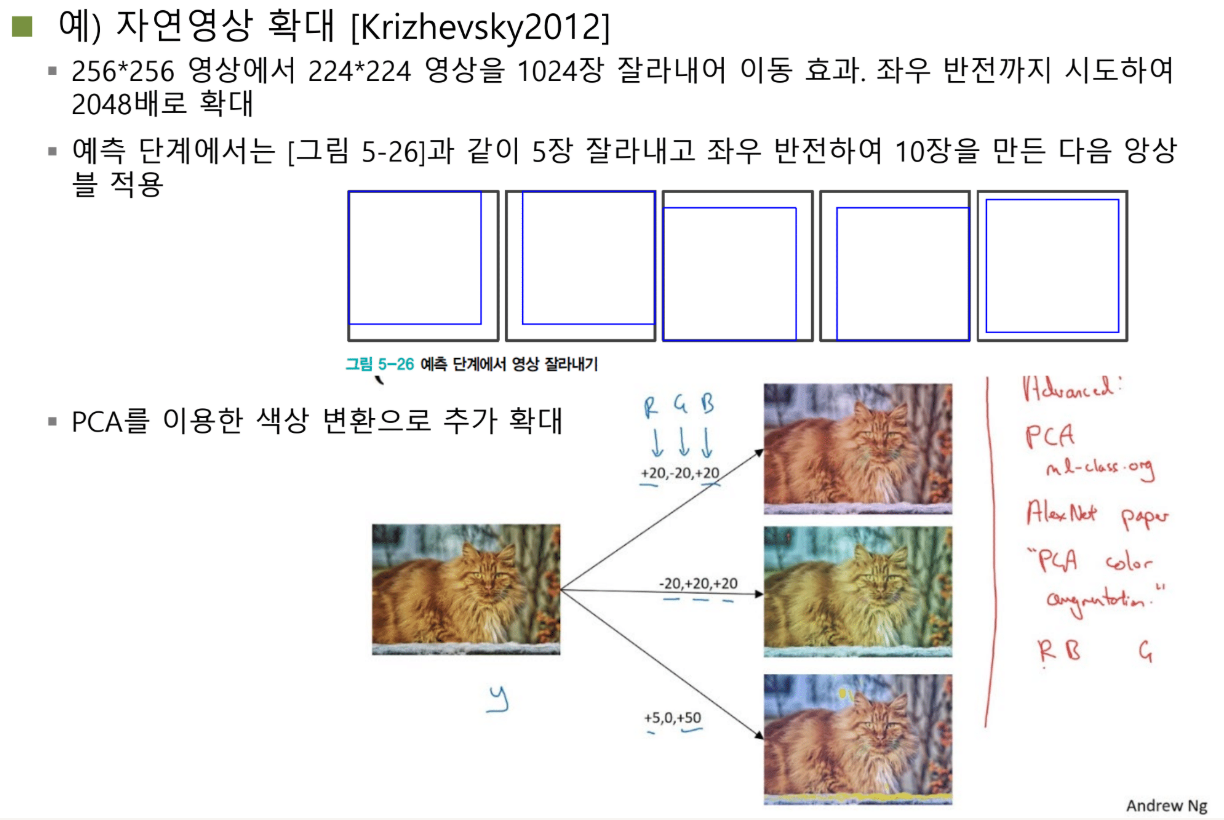
AlexNet은 어떻게 했을까? 256×256 영상을 받아서 224×224로 크롭한다. 크롭 위치를 바꾸면? 왼쪽 상단, 오른쪽 상단, 중앙... 같은 영상에서 1024장을 만든다. 거기에 좌우반전까지 하면? 2048장이다. 한 장에서 2천 배 뻥튀기다.
흥미로운 점은 테스트 시에도 이를 활용한다는 것이다. Test Time Augmentation(TTA). 테스트 이미지 한 장을 받으면 왼쪽 상단, 오른쪽 상단, 왼쪽 하단, 오른쪽 하단, 중앙, 그리고 각각의 반전까지 10장을 만든다. 10장을 모델에 넣어서 나온 출력을 평균낸다.
이것은 앙상블 효과를 낸다. 앙상블은 여러 모델을 쓰는 것인데, 여기서는 모델을 고정하고 입력을 여러 개로 나눈다. 어떤 크롭은 눈을 중점적으로 보고, 어떤 크롭은 코를 본다. 이를 평균내서 판단한다. 생각보다 성능이 꽤 오른다.
PCA 색상 변환
색상도 바꿀 수 있다. 갈색 고양이만 있는 게 아니다. 보라색, 초록색, 핑크색 고양이도 자연에 존재할 수 있다(염색이라도). PCA를 이용한다. RGB 공간에서 픽셀들의 분포를 보고, 그 분포를 가장 잘 대변하는 축을 찾는다. Eigenvalue decomposition과 거의 같다.
이 축상에서 값을 바꾸면 색상이 변한다. R +7, G +15, B -1 이런 식으로. 전체적으로 컬러가 바뀐다. 중요한 것은 PCA를 썼냐가 아니다. 색상을 바꾸는 것도 자연스러운 변형이라는 점이다.
질문이 나왔다. "특정 품종 고양이를 분류할 때도 색상을 바꾸는 게 효과적일까?" 좋은 질문이다. 샴 고양이와 페르시안 고양이를 분류한다고 하자. 색상을 바꾸면 혼란을 주지 않을까?
하지만 생각해보면, 요즘 강아지들을 분홍색이나 녹색으로 염색하지 않나. 고양이도 마찬가지다. 털 색깔이 바뀔 수 있다. 그렇다고 identity가 바뀌는 건 아니다. 따라서 색상 변환도 자연스러운 시뮬레이션이다.
자연을 넘어서: 추상화의 시작
데이터 증강을 연구하다 보니 흥미로운 발견을 했다. 꼭 자연 현상을 모방할 필요가 없다는 것. 비유하자면 이렇다. 하늘을 나는 장치를 만들려던 사람들이 처음에는 새를 모방했다. 날개를 달고 팔로 펄럭였다. 팔만 아프고 안 날았다.
나중에 깨달았다. 중요한 건 날개 모양이나 깃털이 아니었다. 날개 위를 지나가는 바람의 속도와 아래를 지나가는 바람의 속도 차이. 그것이 부양력을 만든다. 원리는 심플하고 추상적이다.
데이터 증강도 마찬가지다. 처음에는 자연 현상을 모방했다. 돌리고, 색깔 바꾸고. 의미 있다. 하지만 자연에서 발생하지 않는 이상한 방식도 효과가 있다는 것을 발견했다.
잡음 기반 증강
Dropout 계열 기법들이다. 픽셀 하나하나에 확률을 준다. 확률값이 특정 임계값 이상이면 0으로 만든다. 얼굴에 검은 점들이 찍힌다. 자연에서 거의 발생하지 않는 왜곡이다. 그런데 학습이 더 잘 된다. 일반화 성능이 높아진다.
Dropout per channel은 RGB 중 하나를 0으로 만든다. 색깔이 바뀌어 총천연색 점들이 다닥다닥 붙는다. Coarse Dropout은 픽셀별이 아니라 블록 단위로 블랙아웃시킨다. Coarse Dropout per channel은 RGB 중 하나를 블록으로 0으로 만든다. 또는 검은색이 아닌 랜덤한 값으로 채운다.
이 모든 경우는 자연에 절대 나타나지 않는다. 인간이 만든 것이다. 그런데 네트워크의 일반화 성능이 올라간다. 신기하지 않은가?

왜 작동하는가?
왜 존재하지도 않는 패턴이 효과가 있을까? 테스트할 때 이런 이미지가 들어올 일도 없는데. 예를 들어보자. 샘플 몇 개로 12차 다항식을 피팅한다. 과적합으로 들쭉날쭉해진다.
여기에 가우시안 노이즈를 추가한다. 각 점 주변에 노이즈 클라우드가 생긴다. 샘플이 엄청 많아진다. 12차 모델이 이를 피팅하려면? 뾰족한 부분이 사라진다. 정확하게 딱 맞지는 않지만, 일반화 성능이 높은 부드러운 곡선이 나온다.
노이즈를 추가해서 학습하는 것은 일반적으로 일반화 성능을 크게 향상시킨다. 직관과 다르지만 효과적이다.
Hyperparameter 최적화: 또 다른 차원의 문제
학습 모델에는 두 종류의 파라미터가 있다. 내부 파라미터와 Hyperparameter. 내부 파라미터는 가중치다. 학습 과정에서 업데이트된다. Hyperparameter는? 학습 전에 미리 결정해야 한다.
학습률, 가중치 감쇠 λ, CNN의 레이어 개수, 필터 개수, Convolution 크기. 이 모든 것이 hyperparameter다. 내부 파라미터 최적화도 중요하지만, hyperparameter 최적화도 성능에 큰 영향을 준다.
레이어를 5개로 할까 10개로 할까? 학습률을 0.1로 할까 1.0으로 할까? 결과가 크게 달라진다. 그렇다면 어떻게 최적화할까?
Hyperparameter 최적화의 어려움
매우 어렵다. 가중치 최적화는 한 번 학습으로 끝난다. 하지만 hyperparameter는? 학습률을 1에서 10으로 바꿨다면 전체를 재학습해야 한다. 또 100으로 바꿨다면? 또 재학습이다.
Hyperparameter를 한 번 바꿀 때마다 그것이 좋은지 판단하는 비용이 너무 크다. 고비용이다. 게다가 미분도 안 된다. 학습률을 미분해서 최적값을 찾을 수 있나? 없다. 레이어 개수를 미분할 수 있나? 없다.

실용적 해결책
가장 좋은 방법은? 표준 문헌이 제시하는 기본값을 사용한다. 남들이 썼던 것을 그대로 쓴다. 보통 몇 가지 후보 값이 있다. 그 값들로 범위를 산정하고, 그 안에서 몇 번 찾아본다.
알고리즘은 이렇다. Q를 검증 성능으로 둔다. 높을수록 좋다. 최댓값을 0으로 초기화한다. Hyperparameter 조합을 생성한다. 학습률 0.1, 모멘텀 0.5, Adam β 0.9 같은 식으로. 모델을 학습한다. 검증 성능을 측정한다. 기존보다 좋으면? Hyperparameter와 성능을 업데이트한다.
여기서 M은 트레이닝 횟수다. Iteration이 아니라 훨씬 큰 단위다. 모델을 한 번 트레이닝하는 것. 한 번에 10시간씩 걸릴 수 있다. Q가 처음에는 올라가고, 안 좋은 hyperparameter로 계속하면 정체하고, 좋은 것을 찾으면 다시 올라간다. 계단식으로 조금씩 개선된다.
격자 탐색 vs 임의 탐색
탐색 구간을 어떻게 설정할까? 두 가지 방법이 있다. 격자 탐색(Grid Search)과 임의 탐색(Random Search).
격자 탐색은 균등 간격으로 샘플링한다. 학습률을 0.1, 0.2, 0.3, 0.4, 0.5로. 모멘텀도 마찬가지로. 격자를 만들어 모든 조합을 시도한다.
임의 탐색은 랜덤하게 뽑는다. 학습률을 Uniform(0, 0.5)에서 랜덤 샘플링. 모멘텀도 마찬가지로. 점들이 불규칙하게 분포한다.
어느 것이 더 좋을까? 놀랍게도 임의 탐색이 더 좋다.

왜 임의 탐색이 우수한가
핵심은 차원의 중요도 차이다. 학습률과 모멘텀 둘 다 hyperparameter지만, 학습률은 성능에 지대한 영향을 준다. 모멘텀은? 0.6을 쓰든 0.7을 쓰든 별 차이가 없다. 어떤 파라미터는 매우 중요하고, 어떤 파라미터는 덜 중요하다.
격자 탐색을 보자. 학습률을 0.2, 0.4, 0.6으로 설정했다면? 학습률 축에서 딱 3개 값만 시도한다. 최적점이 0.3에 있다면? 놓친다.
임의 탐색은? 9개 점이 학습률 축에서 9개의 다른 값을 가진다. 0.3 근처를 탐색할 확률이 훨씬 높다. 모멘텀은 덜 중요하니 상관없다. 결과적으로 중요한 파라미터를 더 다양하게 탐색한다.
일반적으로 임의 탐색이 압도적으로 유리하다. 실제로 훨씬 좋은 결과를 얻었다. 실전에서도 임의 탐색을 쓴다.
로그 스케일과 Proxy
탐색 범위가 0에서 1000이라면? 하지만 대부분 값이 0에서 10 사이에 있을 것 같다면? 로그 스케일을 쓴다. 0, 10, 100, 1000이 0, 1, 2, 3으로 매핑된다. 0에서 10을 촘촘하게, 그 이후를 듬성듬성 탐색한다.
질문이 나왔다. "탐색 자체를 작은 모델로 빠르게 하면?" 좋은 질문이다. 레이어 100개를 10개로, 천만 장을 10만 장으로 줄여서 먼저 탐색한다. 이것을 Proxy Task라고 한다.
주의할 점은 correlation이다. 작은 모델에서 최고였던 것이 큰 모델에서는 5등일 수 있다. 하지만 전체적 경향은 비슷하다. Neural Architecture Search에서 많이 쓴다. 많은 모델 후보를 proxy로 먼저 평가하고, 상위 몇 개만 실제로 학습한다. 실용적 타협이다.
마무리: 규제의 생태계
암시적 규제는 직접적이지 않지만 효과적이다. 조기 멈춤은 간단하지만 강력하다. 참을성과 세대 반복 인자로 현실에 맞게 조정한다. 데이터 증강은 가장 확실한 해결책이다. 자연 현상을 모방하다가, 이제는 추상적 원리로 발전했다. 자연에 없는 노이즈도 효과적이다.
Saliency Mix 같은 연구는 문제를 발견하고 해결하는 과정이다. 연구는 거창하지 않다. 이상한 것을 발견하고 고치는 것. 그것이 연구다. Hyperparameter 최적화는 또 다른 차원의 문제다. 고비용이고 미분 불가능하다. 임의 탐색이 놀랍게도 격자 탐색보다 우수하다.
모든 규제 기법들은 하나의 목표를 향한다. 일반화 성능을 높이는 것. 모델이 훈련 데이터를 암기하지 않고 진정으로 이해하게 만드는 것. 명시적이든 암시적이든, 직접적이든 간접적이든, 결과적으로 과적합을 막으면 된다. 그것이 규제의 본질이다.
딥러닝은 이 모든 기법들의 총합이다. 좋은 구조, 좋은 최적화, 좋은 규제. 이 삼박자가 맞아야 훌륭한 모델이 탄생한다. 특히 데이터가 부족할 때, 규제의 중요성은 더욱 커진다. 결국 우리는 제한된 자원으로 최선을 만들어내야 한다. 그것이 엔지니어링이고, 그것이 연구다.