밀도 추정과 Gaussian Mixture Model
밀도 추정이란 무엇인가
지난 시간에 군집화를 배웠습니다. 오늘은 비슷하지만 목적이 다른 밀도 추정을 다룹니다.
군집화는 "이 샘플이 어느 그룹에 속하는가?"를 묻습니다. 분류 문제죠.
밀도 추정은 "이 샘플들이 원래 어떤 분포에서 왔는가?"를 묻습니다. 예를 들어, 주사위를 6만 번 던져서 각 숫자가 만 번씩 나왔다면, 우리는 P(X) = 1/6 이라고 추정할 수 있습니다.
분포를 알면 뭐가 좋을까요? 새로운 샘플을 무한히 생성할 수 있습니다. 이게 생성 모델의 출발점입니다.
첫 번째 시도: Histogram
가장 단순한 방법은 Histogram입니다. 특징 공간을 격자로 나눕니다. 예를 들어 0.1씩 간격으로 칸을 만듭니다. 그리고 각 칸에 샘플이 몇 개 들어있는지 세는 거죠.
칸 A: 샘플 4개 → 4/80 = 5%
칸 B: 샘플 40개 → 40/80 = 50%
새로운 점이 주어지면? 그 점이 속한 칸의 확률을 반환합니다. 직관적이죠.
문제: 계단 모양
그런데 심각한 문제가 있습니다. 경계선에서 확률이 급격히 변합니다.
P(x = 0.001) = 10%
P(x = -0.001) = 50%
0.2mm 차이인데 확률이 5배 차이입니다. 키가 0.2mm 바뀐다고 확률이 이렇게 달라질 리 없죠. 이게 계단 모양 함수의 문제입니다.
칸 크기 문제
칸을 촘촘하게 나누면? 많은 칸이 비어있습니다. 들쭉날쭉한 분포가 나오죠. 과적합입니다.
칸을 크게 나누면? 모든 칸이 비슷한 확률을 갖습니다. 의미 있는 패턴이 사라져요. 과소적합입니다.
적절한 칸 크기를 찾는 것 자체가 어려운 문제입니다.

Kernel Density Estimation: 부드럽게 만들기
계단을 없애려면 어떻게 해야 할까요? 점을 면적으로 바꾸는 겁니다.
씨앗이 있다고 생각해보세요. 그 씨앗 위에 찰흙을 붙입니다. 점이 2차원 면적이 되죠. 여러 점에 찰흙을 붙여서 모으면 하나의 큰 덩어리가 됩니다. 이게 확률밀도함수입니다.
수학적으로는 각 점에 '커널(kernel)'이라는 함수를 씌웁니다.
p(x) = (1/nh^d) Σᵢ K((x - xᵢ)/h)
여기서:
- K는 커널 함수
- h는 bandwidth (커널의 폭)
- n은 샘플 개수, d는 차원
작동 방식은 간단합니다. 각 샘플 xᵢ에 커널을 씌워요. 그리고 점 x에서 모든 커널의 값을 합산합니다. 샘플이 많이 모인 곳은 커널이 많이 겹치니까 밀도가 높아지죠.
정사각형 커널의 문제
학생이 좋은 질문을 했습니다: "커널을 씌워도 여전히 계단 아닌가요?"
맞습니다. 정사각형 커널을 쓰면 여전히 계단입니다. Histogram보다는 부드럽지만 각진 부분이 남아요.
해결책은? 가우시안 커널을 씁니다.
K(u) = (1/√(2π)) exp(-u²/2)
이제 각진 부분이 없습니다. 여러 가우시안이 겹치면 매끄러운 확률밀도함수가 만들어집니다.
Bandwidth 문제
그런데 Histogram의 칸 크기 문제가 사라진 건 아닙니다. 이제 이름만 bandwidth h로 바뀌었어요.
h가 너무 작으면 커널이 좁고 뾰족합니다. 들쭉날쭉한 분포가 나와요. 과적합이죠.
h가 너무 크면 커널이 넓고 완만합니다. 모든 게 뭉개집니다. 과소적합입니다.
근본적 한계
더 심각한 문제가 있습니다.
첫째, 모든 샘플을 저장해야 합니다. 새로운 점 x가 주어지면 모든 샘플과의 거리를 계산해야 해요. 샘플이 천만 개면 천만 번 계산입니다. 현대 딥러닝처럼 수백만 장의 이미지를 다루는 문제에서는 실용적이지 않습니다.
둘째, 차원의 저주입니다. 차원이 하나 늘 때마다 같은 밀도를 유지하려면 샘플 개수가 지수적으로 증가해야 합니다. 2차원에서 100개로 충분했다면, 3차원에서는 1,000개, 10차원에서는 100억 개가 필요합니다. MNIST는 784차원인데, 이건 물리적으로 불가능한 수준이에요.
학생이 또 질문했습니다: "샘플을 정규화해야 하나요?"
네, 해야 합니다. 키는 cm 단위고 몸무게는 kg 단위죠. 단위가 다르면 거리 계산이 공정하지 않습니다. 정규화하면 평균 μ와 표준편차 σ를 저장해두고 나중에 원래 스케일로 복원할 수 있어요.
Parametric Method: 발상의 전환
그럼 어떻게 해야 할까요? 발상을 바꿔봅시다.
1억 명의 키 데이터가 있다고 하죠. 1억 개 값을 전부 저장하는 대신, 평균과 분산 두 개 값만 저장하면 어떨까요?
평균 μ = 172cm
분산 σ² = 25cm²
이 두 개 값으로 1억 명의 분포를 표현합니다. 메모리가 1억분의 1로 줄었어요. 이게 **모수적 방법(Parametric Method)**입니다. 샘플을 직접 저장하지 않고, 그 샘플을 대표하는 파라미터만 저장하는 거죠.
단봉 분포, 그러니까 산이 하나인 분포에서는 잘 작동합니다. 키 분포가 평균 172cm, 표준편차 5cm라면 N(172, 5²)로 완벽하게 표현되죠.
다봉 분포의 문제
그런데 이런 경우는 어떨까요?
●●● ●●●
● ● ● ●
● ● ● ●
산이 두 개입니다. 남성 평균 175cm, 여성 평균 162cm처럼 두 개의 봉우리가 있는 분포죠.
가우시안 하나로 피팅하면 중간에 큰 산 하나가 예측됩니다. 실제로는 샘플이 거의 없는 곳이 가장 확률 높은 곳으로 나와요. 완전히 틀렸습니다.
해결책은? 가우시안을 여러 개 쓰는 겁니다. 이게 Gaussian Mixture Model입니다.
Gaussian Mixture Model
분포에 봉우리가 k개 있으면 가우시안을 k개 사용합니다.
p(x) = Σⱼ₌₁ᵏ πⱼ · N(x | μⱼ, σⱼ²)
πⱼ는 j번째 가우시안의 비중입니다. 전체에서 차지하는 비율이죠. 당연히 합이 1이어야 합니다.
분포 = 0.6 × 가우시안1 + 0.4 × 가우시안2
첫 번째 가우시안이 60%, 두 번째가 40%를 차지한다는 뜻입니다.
파라미터가 늘었습니다. 평균 k개, 분산 k개, 비중 k개. 총 3k개죠. 복잡도는 늘었지만 훨씬 풍부한 분포를 표현할 수 있습니다.

추정 문제
이제 문제는 주어진 샘플로부터 이 파라미터들을 어떻게 찾느냐입니다.
Maximum Likelihood Estimation을 씁니다. 샘플들이 발생할 likelihood를 최대화하는 θ를 찾는 거죠.
θ* = argmax_θ Σ log p(xᵢ | θ)
문제는 이 식을 직접 미분해서 풀 수 없다는 겁니다. 가우시안이 여러 개 섞여있어서 수식이 너무 복잡해요. 그래서 EM 알고리즘을 사용합니다.
GMM의 EM 알고리즘
K-means와의 관계
GMM은 K-means와 놀랍도록 비슷합니다.
K-means:
- A: 각 샘플의 군집 소속 (hard label)
- X₁: [1, 0] 첫 번째 군집
- X₂: [0, 1] 두 번째 군집
- C: 각 군집의 중심
GMM:
- Z: 각 샘플의 가우시안 소속 확률 (soft label)
- X₁: [0.7, 0.3] 70% 첫 번째, 30% 두 번째
- X₂: [0.1, 0.9] 10% 첫 번째, 90% 두 번째
- θ = {π, μ, σ}: 각 가우시안의 파라미터
핵심 차이는 두 가지입니다.
- Hard vs Soft: K-means는 "너는 1번", GMM은 "70% 확률로 1번"
- 목적이 다름: K-means는 A를 얻는 게 목적이고, GMM은 θ를 얻는 게 목적
EM의 두 단계
먼저 θ를 랜덤하게 초기화합니다. 그리고 두 단계를 반복합니다.
E-step (Expectation): Z 추정하기 M-step (Maximization): θ 업데이트하기
K-means에서 E-step은 A를 할당하고 M-step은 C를 평균 계산했죠? GMM에서는 역할이 바뀝니다. 왜냐하면 목적이 다르거든요.
E-step 상세
현재 파라미터 θ로 각 샘플이 각 가우시안에 속할 확률을 계산합니다.
샘플이 X₁, X₂, X₃ 세 개 있고, 가우시안이 Blue, Red 두 개 있다고 해봅시다.
1단계: Raw 확률 계산
각 샘플을 각 가우시안에 넣어봅니다.
Z_raw[i,j] = πⱼ × N(xᵢ | μⱼ, σⱼ²)
예를 들어:
Blue Red
X₁: 0.15 0.05 (Blue에 가까움)
X₂: 0.05 0.05 (중간)
X₃: 0.05 0.15 (Red에 가까움)
2단계: 행별로 정규화
각 샘플에 대해 모든 가우시안의 확률 합이 1이 되도록 만듭니다.
Z[i,j] = Z_raw[i,j] / (Z_raw[i,1] + Z_raw[i,2])
결과:
Blue Red
X₁: 0.75 0.25 (75% Blue)
X₂: 0.50 0.50 (중립)
X₃: 0.25 0.75 (75% Red)
이게 E-step입니다. X₁은 75% 확률로 Blue 가우시안에서 왔다는 뜻이죠.
M-step 상세
이제 Z를 가중치로 사용해서 파라미터를 업데이트합니다.
평균 업데이트:
μⱼ = Σᵢ Z[i,j] × xᵢ / Σᵢ Z[i,j]
Blue 가우시안의 평균을 예로 들면:
분자 = 0.75×X₁ + 0.50×X₂ + 0.25×X₃
분모 = 0.75 + 0.50 + 0.25 = 1.5
μ_Blue = 분자 / 1.5
직관적으로 X₁은 75% 가중치로 평균에 기여하고, X₃는 25% 가중치로만 기여합니다. Blue에 더 속한 샘플이 평균에 더 영향을 주는 거죠.
분산 업데이트:
σⱼ² = Σᵢ Z[i,j] × (xᵢ - μⱼ)² / Σᵢ Z[i,j]
마찬가지로 가중 분산입니다.
비중 업데이트:
πⱼ = (1/n) Σᵢ Z[i,j]
Blue 열의 합은 0.75 + 0.50 + 0.25 = 1.5입니다. 전체 샘플이 3개니까:
π_Blue = 1.5/3 = 0.5
Blue 가우시안이 전체의 50%를 차지한다는 뜻입니다.

K-means와 비교
정리해봅시다.
K-means GMM
| 소속 정보 | A (hard: [1,0]) | Z (soft: [0.7,0.3]) |
| 파라미터 | C (중심) | θ = {π,μ,σ} |
| E-step | A 할당 | Z 확률 계산 |
| M-step | C 평균 | θ 가중평균 |
| 목적 | A 찾기 | θ 찾기 |
역할이 반전된 이유는 목적이 다르기 때문입니다. K-means는 A(소속)를 찾고 싶어서 C(중심)를 수단으로 씁니다. GMM은 θ(파라미터)를 찾고 싶어서 Z(소속)를 수단으로 쓰는 거죠.
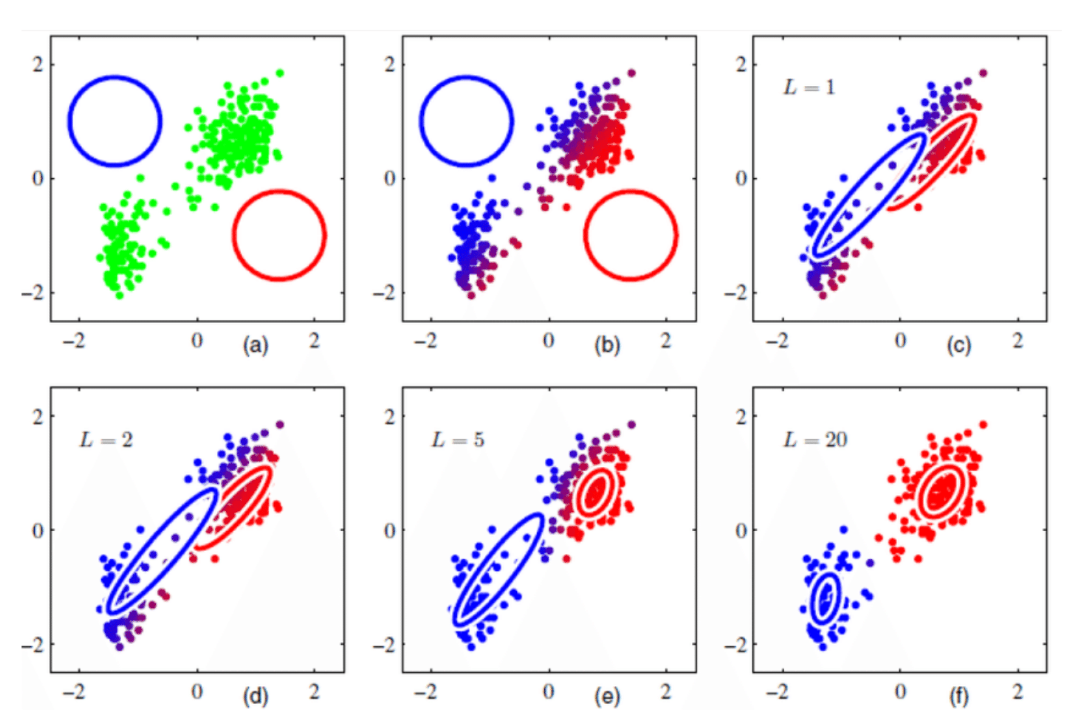
시각화
초기에는 두 가우시안이 랜덤 위치에 있고 샘플들은 회색입니다. 어디에 속할지 모르거든요.
Iteration이 진행되면서:
- E-step에서 각 샘플이 파란빛이나 붉은빛을 띠기 시작합니다
- M-step에서 가우시안들이 샘플 군집으로 이동합니다
10번쯤 반복하면 Blue 가우시안은 왼쪽 군집에, Red 가우시안은 오른쪽 군집에 정확히 위치합니다. 샘플 색깔도 명확해지죠.
수학적으로 보장됩니다. K-means처럼 GMM도 iteration마다 likelihood가 단조증가합니다. 절대 나빠지지 않아요.
GMM의 장점
GMM은 K-means보다 더 많은 정보를 제공합니다.
- 밀도 추정: p(x) = Σ πⱼN(x|μⱼ,σⱼ²) 로 새 샘플 생성 가능
- Soft clustering: Z를 보면 확률적 소속 정보
- Hard clustering: Z에서 argmax 취하면 K-means와 똑같음
GMM으로 K-means를 대체할 수 있습니다. 역은 안 돼요.
공간 변환과 인코더-디코더
비지도학습의 세 번째 과업인 공간 변환을 살펴봅시다.
문제: 선형 분리 불가능
원형 분포를 생각해보세요.
●●●●●
● ●
● ○○○ ●
● ○ ●
●●●●●
안쪽 원 ○와 바깥쪽 링 ●를 직선으로 나눌 수 없습니다.
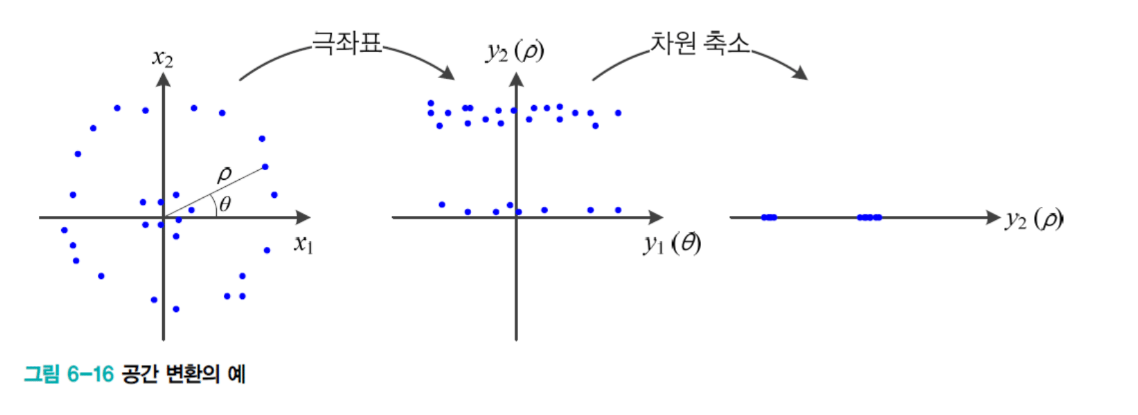
극좌표 변환
(x₁, x₂)를 (θ, r)로 바꿔봅시다. θ는 각도, r은 원점으로부터 거리입니다.
변환하면:
r축
↑
●●●●●●●● (바깥 링, r 큼)
---------- (이제 직선으로 분리!)
○○○○○○○○ (안쪽 원, r 작음)
선형 분리 가능해졌습니다. 여기서 θ 축을 제거하면 2차원이 1차원이 됩니다. 정보 손실은 거의 없어요. r만으로도 충분히 구분되거든요.
인코더-디코더 구조
X (원본) → Encoder → Z (은닉) → Decoder → X̂ (복원)
Encoder는 원래 공간을 은닉 공간으로 변환합니다. Decoder는 다시 원래 공간으로 복원하죠.
유튜브를 생각하면 됩니다. 서버에 4K 영상이 있으면, 이걸 압축된 비트스트림으로 만들어 전송합니다. 사용자 컴퓨터에서 다시 4K 영상으로 복원하는 거죠.
목적에 따른 설계
데이터 압축:
- Z 차원을 X보다 훨씬 작게
- 목표: X ≈ X̂ (복원 품질)
- 10MB를 1MB로 압축, 다시 10MB로 복원
데이터 시각화:
- Z 차원 = 2 or 3
- 목표: 구조 보존
- 784차원 MNIST를 2차원 평면에 투영
특징 추출:
- Z 차원 = 적절히 작게
- 목표: 의미 있는 특징만
- 다운스트림 작업에 Z 사용
생성 모델:
- Z를 확률 공간으로
- Z에서 샘플링해서 새 X 생성
- 두 샘플 사이 보간 가능
왜 작동하는가
매니폴드 가정 때문입니다. 784차원 전체가 의미 있는 게 아니라 그 안의 10차원 매니폴드에 실제 데이터가 분포합니다. Encoder가 이 매니폴드를 찾아내고, Z가 매니폴드 상의 좌표가 되는 거죠.
병목(bottleneck)이 필터 역할을 합니다. 중요한 정보만 Z를 통과하고, 중복이나 노이즈는 걸러집니다.
다음 시간에는 Autoencoder, VAE 같은 구체적인 방법들을 배웁니다.
복습 질문
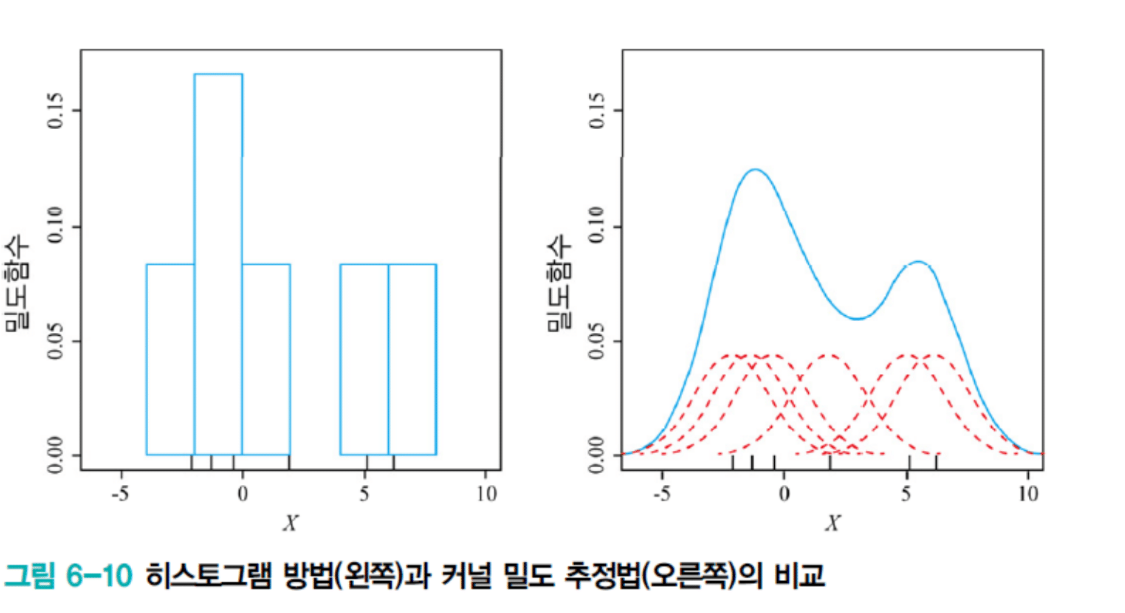
1. Histogram과 Kernel Density Estimation의 공통점과 차이점
공통점을 먼저 봅시다.
둘 다 밀도를 추정합니다. 관측된 샘플로부터 확률분포 p(x)를 역추정하죠. 그리고 둘 다 hyperparameter에 민감합니다. Histogram은 칸 크기, KDE는 bandwidth h. 이 값에 따라 과적합이나 과소적합이 발생해요. 또 둘 다 비모수적 방법입니다. 특정 분포를 가정하지 않고 데이터가 말하게 하죠.
차이점을 볼까요.
Histogram은 칸 안의 샘플 개수를 셉니다. 그래서 불연속적이에요. 계단 모양이죠. 경계 문제가 심각합니다. x=0.001과 x=-0.001이 5배 차이날 수 있어요.
KDE는 커널의 가중합을 계산합니다. 특히 가우시안 커널을 쓰면 연속적입니다. 경계가 부드럽게 변하죠.
구체적인 예를 들어봅시다:
Histogram:
P(x = 0.001) = 10%
P(x = -0.001) = 50%
0.2mm 차이인데 확률이 5배. 말이 안 되죠.
KDE:
P(x) = (1/nh) Σ K((x-xᵢ)/h)
가우시안 커널 쓰면 부드럽게 변합니다.
여전한 공통 약점도 있습니다.
둘 다 모든 샘플을 저장해야 합니다. 메모리가 폭발하죠. 그리고 둘 다 차원의 저주에 시달립니다. 고차원에서는 작동하지 않아요. Hyperparameter 튜닝도 둘 다 어렵습니다.
2. GMM의 E-step과 M-step, K-means와의 차이
GMM의 목표는 파라미터 θ = {π, μ, σ}를 추정하는 겁니다. π는 각 가우시안의 비중, μ는 평균, σ는 표준편차죠.
E-step에서는 소속 확률 행렬 Z를 추정합니다.
1단계로 raw 확률을 계산합니다:
Z_raw[i,j] = πⱼ × N(xᵢ | μⱼ, σⱼ²)
2단계로 행별로 정규화합니다:
Z[i,j] = Z_raw[i,j] / sum(Z_raw[i,:])
결과가 이렇게 나옵니다:
가우시안1 가우시안2
샘플1: 0.75 0.25
샘플2: 0.50 0.50
샘플3: 0.25 0.75
샘플1은 75% 확률로 가우시안1에서 왔다는 뜻이죠.
M-step에서는 Z를 가중치로 사용해서 θ를 업데이트합니다.
평균:
μⱼ = Σᵢ (Z[i,j] × xᵢ) / Σᵢ Z[i,j]
분산:
σⱼ² = Σᵢ (Z[i,j] × (xᵢ-μⱼ)²) / Σᵢ Z[i,j]
비중:
πⱼ = (1/n) Σᵢ Z[i,j]
가중 평균이에요. 높은 소속 확률이 높은 가중치가 되는 거죠.
K-means와 비교해봅시다.
K-means GMM
| 최종 목표 | A (군집 소속) | θ (분포 파라미터) |
| 은닉 변수 | C (군집 중심) | Z (소속 확률) |
| E-step | A 할당 | Z 계산 |
| M-step | C 평균 | θ 가중평균 |
| 라벨 | [1,0] or [0,1] | [0.7, 0.3] |
E/M 역할이 왜 반대일까요? 목적이 다르기 때문입니다.
K-means는 A를 얻는 게 목적이고 C는 수단입니다. 그래서 E에서 A를 추정하죠.
GMM은 θ를 얻는 게 목적이고 Z는 수단입니다. 그래서 M에서 θ를 추정합니다.
구조는 같지만 목적이 다르니까 역할이 뒤바뀐 거예요.
GMM의 추가 장점도 있습니다.
Soft clustering이 가능합니다. "60%는 그룹1, 40%는 그룹2"처럼 불확실성을 표현할 수 있어요.
밀도 추정도 됩니다:
p(x) = Σⱼ πⱼ N(x|μⱼ,σⱼ²)
새 샘플을 생성할 수 있죠.
K-means도 대체 가능합니다. Z에서 argmax 취하면 hard label이 되거든요. GMM이 훨씬 다재다능합니다.
3. KDE의 한계와 Parametric Method의 해결
KDE의 근본적 한계를 두 가지 봅시다.
첫 번째, 모든 샘플을 저장해야 합니다.
새로운 점 x가 주어지면 모든 샘플과의 거리를 계산해야 해요:
def kde_density(x_new, samples, h):
total = 0
for x_i in samples:
total += kernel((x_new - x_i) / h)
return total / (len(samples) * h)
샘플이 100개면 100번, 천만 개면 천만 번 계산입니다. 메모리는 O(n), 계산은 O(n) per query죠.
실제로 ImageNet은 100만 장 이미지에 각 784차원입니다. 7.84억 개 값을 저장해야 하고, 쿼리당 7.84억 번 커널을 계산해야 해요. 현대 규모에서는 실용 불가능합니다.
두 번째, 차원의 저주입니다.
1차원에서 밀도 0.1을 유지하려면 10개 샘플이 필요합니다. 2차원에서는 10² = 100개, 3차원에서는 10³ = 1,000개죠. d차원에서는 10^d 개가 필요해요.
MNIST는 784차원인데, 10^784 개 샘플이 필요합니다. 우주의 원자 개수가 10^80개 정도인데, 이건 물리적으로 불가능한 수준입니다.
Parametric Method가 어떻게 해결할까요?
핵심 아이디어는 샘플을 직접 저장하지 말고 대표 파라미터만 저장하는 겁니다.
# KDE 방식
samples = [170, 165, 180, 175, ...] # 1억 개 저장
# Parametric 방식
mu = 172
sigma = 5
# 단 2개 값으로 1억 개 표현!
저장 공간이 O(n)에서 O(1)로, 쿼리 시간도 O(n)에서 O(1)로 줍니다. GMM은 3k개 파라미터로 수백만 샘플을 표현할 수 있어요.
차원의 저주도 완화됩니다. KDE는 10차원에서 10^10 샘플이 필요하지만, GMM은 파라미터 개수가 똑같습니다. 샘플 개수와 독립적이죠.
4. GMM에서 πⱼ의 역할
πⱼ는 j번째 가우시안의 상대적 비중입니다. 전체에서 차지하는 비율이죠.
두 색깔 물감을 섞는다고 생각해보세요. 파란 물감 60%, 빨간 물감 40%를 섞으면 보라색이 됩니다. π₁ = 0.6, π₂ = 0.4죠.
GMM도 마찬가지입니다:
p(x) = 0.6 × 가우시안1 + 0.4 × 가우시안2
전체 분포에서 60% 샘플이 가우시안1에서 나오고, 40%가 가우시안2에서 나옵니다.
왜 Σπⱼ = 1일까요?
확률의 공리 때문입니다. 확률분포는 전체 면적이 1이어야 하죠:
∫ p(x) dx = 1
GMM에서 계산하면:
∫ Σⱼ πⱼ N(x|μⱼ,σⱼ²) dx = Σⱼ πⱼ × 1 = Σⱼ πⱼ
각 가우시안의 면적은 1이니까, 결국 Σπⱼ = 1이어야 전체 면적이 1입니다.
또 다른 관점으로, 모든 샘플은 어딘가에 속해야 합니다:
P(가우시안1) + P(가우시안2) + ... = 100%
π₁ + π₂ + ... = 1
계산은 간단합니다:
πⱼ = (1/n) × (Z 행렬 j번째 열의 합)
예를 들어 Blue 열의 합이 1.5이고 전체 샘플이 3개면, π_Blue = 1.5/3 = 0.5입니다.
5. 인코더-디코더의 역할과 목적별 설계
인코더-디코더의 기본 구조는 이렇습니다:
X (원본) → Encoder → Z (은닉) → Decoder → X̂ (복원)
Encoder는 원래 특징 공간을 은닉 공간으로 변환하고, Decoder는 다시 원래 공간으로 복원합니다.
목적에 따라 설계가 달라집니다.
데이터 압축이 목적이면:
- Z 차원을 훨씬 작게 만듭니다
- 목표는 X ≈ X̂ (복원 품질)
- 10MB를 1MB로 압축했다가 다시 10MB로 복원하는 거죠
데이터 시각화가 목적이면:
- Z 차원을 2 or 3으로 만듭니다
- 목표는 구조 보존
- 784차원 MNIST를 2차원 평면에 그려서 사람이 볼 수 있게 하는 겁니다
특징 추출이 목적이면:
- Z 차원을 적절히 작게 만듭니다
- 목표는 의미 있는 특징만 남기기
- 다운스트림 작업에 Z를 사용하죠
생성 모델이 목적이면:
- Z를 확률 공간으로 만듭니다
- Z에서 샘플링해서 새 X를 생성합니다
- 두 샘플 사이를 보간할 수도 있어요
왜 작동할까요?
매니폴드 가정 때문입니다. 784차원 전체가 의미 있는 게 아니라, 그 안의 10차원 매니폴드에 실제 데이터가 분포합니다. Encoder가 이 매니폴드를 찾아내고, Z가 매니폴드 상의 좌표가 되는 거죠.
병목(bottleneck)이 필터 역할을 합니다. 중요한 정보만 Z를 통과하고, 중복이나 노이즈는 걸러집니다.