메모리의 마법: LSTM에서 현대 Transformer까지
프롤로그: RNN의 치명적 약점
지난 시간에 우리는 RNN의 근본적인 문제를 봤습니다. 정보 희석이었죠.
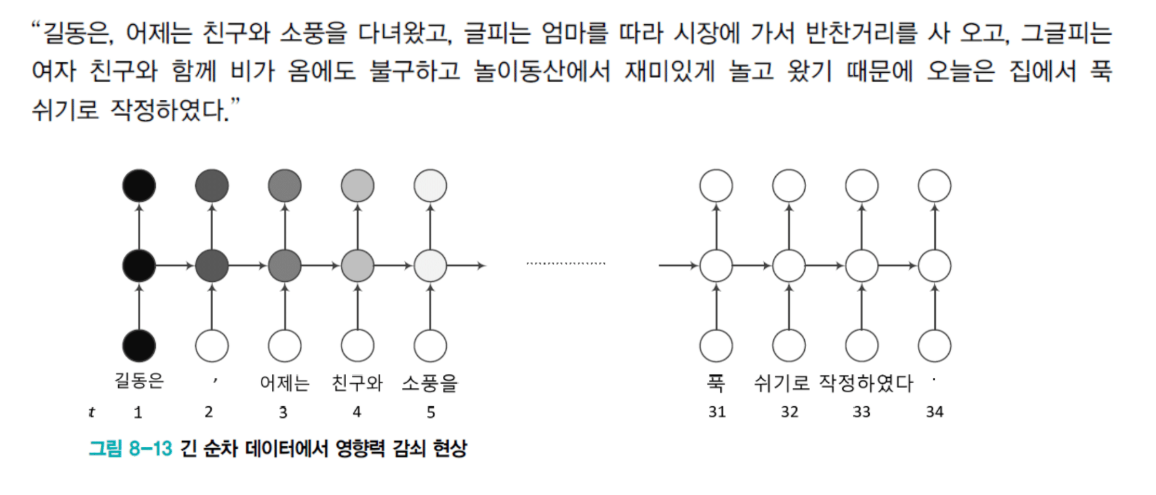
"길동은 어제 친구랑 소풍을 다녀왔고 그 다음날은 엄마를 따라갔고 그 다음날은 여자친구랑 놀이동산에서 놀았기 때문에 오늘은 집에서 푹 쉬기로 했다."
이 문장에서 **"길동은"**이라는 주어와 **"쉬기로"**라는 동사가 연결되어야 합니다. 하지만 그 사이에 수많은 단어가 끼어있죠.
RNN의 문제는 이겁니다. H(은닉 벡터)가 하나밖에 없는데, 이 H가 계속 W와 곱해지고 새로운 입력과 더해지면서 처음의 "길동은" 정보가 점점 희석됩니다. 푹 쉬기로 할 때쯤 가면 "길동은"은 온데간데없고, 누가 쉬었는지조차 모르는 상황이 발생하는 거죠.
이건 RNN의 구조적 문제입니다. 피할 수 없어요.
학습할 때도 마찬가지입니다. Gradient vanishing이 심각하죠. 끝에서 발생한 gradient가 앞으로 전달되려면 30개의 레이어를 역으로 거슬러 올라가야 하는데, 전달이 거의 안 됩니다.
결과: 마지막 T 시점의 입력-출력에 대해서는 U, W, V가 강하게 학습되지만, 앞쪽 단어들에 대해서는 학습이 거의 안 됩니다.
반대로 gradient 폭발도 발생할 수 있습니다. W의 norm이 굉장히 큰 경우, H 값이 계속 곱해지면서 점점 커지는 현상이죠.
RNN은 긴 입력 샘플이 자주 발생하기 때문에 이런 현상들이 Deep MLP나 CNN보다 훨씬 더 심각합니다. 게다가 가중치 공유 때문에 - W라는 한 녀석 때문에 - 값이 엄청나게 줄어들거나 폭발하는 문제가 가속화됩니다.
이 문제를 해결하기 위해 드디어 LSTM이 등장했습니다.
BPTT: 시간을 거슬러 올라가는 학습
RNN의 학습 알고리즘
RNN을 학습하는 방법을 BPTT라고 부릅니다.
- B: Back
- P: Propagation
- TT: Through Time
시간에 걸쳐서 backpropagation을 한다는 뜻입니다.
근본적으로는 MLP와 완전히 동일한데, 시간에 따라서 출력값이 계속 바뀌기 때문에 그거를 좀 고려한 방법이라고 보시면 됩니다.
Deep MLP vs RNN: 놀라운 유사성
RNN과 Deep MLP는 굉장히 유사합니다. 거의 동일하다고 볼 수 있어요.
특히 은닉 노드 부분을 잘 보세요:
H₁ → H₂ → H₃ → ...
- 첫 번째 히든 노드의 값이 → 두 번째 히든 레이어로
- 두 번째 히든 레이어가 → 세 번째 히든 레이어로
X가 중간에 튀어나오고 Y가 튀어 들어가고 Y가 튀어나온다는 점을 제외하면, 이 부분만 따서 표현하면 Deep MLP와 동일한 형태로 표현 가능합니다.
두 가지 결정적 차이
그런데 차이점이 있습니다. 뭘까요?
차이점 1: 가중치 공유
Deep MLP로 표현하기에 한계가 있어요.
RNN: 첫 번째 히든 벡터가 두 번째 히든 벡터로 갈 때 W 사용, 두 번째가 세 번째로 갈 때도 동일한 W 공유
Deep MLP: 각 레이어들이 같은 가중치를 공유할 이유가 없죠. 당연히 다릅니다.
차이점 2: 가변 길이
RNN: 입력 길이에 따라 가변 입력 길이를 적응할 수 있어요.
- 입력 길이가 7개 → 7개 레이어를 쌓은 것과 같은 효과
- 입력 길이가 3개 → 3개 레이어를 쌓은 것과 같은 효과
Deep MLP: 한번 레이어 개수가 정해지면 바꿀 수가 없습니다.
정리:
- RNN: 샘플마다 은닉층의 수가 다른 것으로 볼 수 있음
- Deep MLP: 왼쪽에 입력, 오른쪽에 출력
- RNN: 매 순간 입력과 출력이 나옴
- RNN: 가중치를 공유
- Deep MLP: 각 layer마다 가중치가 다름

목적 함수: 시간 축을 따라 더하기
목적 함수도 CNN에서 사용하던 것을 거의 그대로 쓸 수 있습니다.
단 한 가지 차이: 출력값이 시간에 따라 달라지고, 그 시간에 따라 다른 출력값에 대응되는 Ground Truth 목표값도 다릅니다.
J = J₁ + J₂ + J₃ + ... + Jₜ
한 시점에서의 목적함수 값을 계산하는 것뿐만 아니라, 1번 시점부터 전체 T 시점까지의 전체 시점에 대한 목적함수 값을 구해서 다 더하는 형태로 최종 목적 함수를 만듭니다.
어렵지 않죠? 그냥 loss가 발생하는 곳의 loss 값을 쭉 더하는 거예요.
Loss 함수 선택
J를 여러 방법으로 모델링할 수 있습니다:
- Mean Square Error (MSE)
- Cross Entropy
- Negative Log Likelihood
일반적으로는 Cross Entropy를 많이 사용합니다.
왜? Ground Truth word 자체가 원핫 벡터잖아요. 우리가 예측한 값도 합이 1이 되는 확률적인 softmax를 통과한 값이기 때문에 둘 다 확률분포입니다.
두 확률분포 간의 차이를 최소화하는 가장 좋은 메트릭이 교차 엔트로피이기 때문이죠.
Gradient 계산
그래디언트 계산은 여러분이 알고 있는 수학식을 이용해서 집어넣어보면 그대로 나오는 형태입니다.
제가 "gradient 계산하시오" 같은 문제는 안 낼 테니까, 머리 싸매고 공부하실 필요까지는 없는 것 같아요. 중요한 부분은 아니라고 생각했습니다.
5세트의 가중치
어쨌든 gradient는 결국 U, W, V, b, c에 대해서 계산합니다:
- U: 입력층의 가중치
- b: 입력층의 bias
- W: 은닉층에서 다음 시점 은닉층으로 이동할 때의 가중치 (hₜ₋₁ → hₜ)
- V: 출력층의 가중치
- c: 출력층의 bias
총 5세트의 가중치들을 목적 함수에 대해서 미분한 gradient 값을 계산하면 됩니다.
V에 대한 Gradient: 가장 쉬운 것부터
V는 출력에만 영향을 주기 때문에 가장 계산하기 쉽습니다.
V에 대한 gradient는 당연히 V matrix의 크기와 동일한 크기의 matrix를 가지겠죠. 이것들을 다 모아놓은 걸 **자코비안(Jacobian)**이라고 부릅니다.
예제: V₁₂에 대한 Gradient
구체적으로 V₁₂라는 매개변수로 미분한 gradient를 한번 구해봅시다.
입력: x₁, x₂
은닉: h₁, h₂, h₃ (3차원 벡터)
출력: o₁, o₂
V₁₂는 두 번째 H로부터 첫 번째 O로 맵핑시켜줄 때 h₂에 곱해지는 값입니다.
o₁ = V₁₁·h₁ + V₁₂·h₂ + V₁₃·h₃
V₁₂가 여기서도 loss가 걸려 있고, 여기서도 loss가 걸려 있고... 모든 시점에서 gradient가 발생합니다.




Chain Rule 적용
목적 함수에는 V₁₂가 explicitly하게 나타나지 않습니다. V₁₂는 과거 함수에서 계산되고, 그 출력 결과의 출력 결과가 목적 함수로 들어간 형태이기 때문에 외재적으로는 V₁₂를 관측할 수 없죠.
따라서 chain rule을 사용해서 local gradient를 구해서 V₁₂에 대한 미분값을 얻습니다.
H → O → softmax → Y' → Loss(J)
각 단계의 local gradient를 구해서:
- O에 대한 local gradient
- Softmax에 대한 local gradient
- Loss에 대한 local gradient
이것들을 다 곱하면 ∂J/∂V₁₂가 나옵니다.
Softmax와 Log의 미분
Y'는 결국 softmax 함수입니다:
y' = softmax(o) = exp(oᵢ) / Σexp(oⱼ)
목적함수는 마이너스 로그:
J = -log(y')
이걸 미분하면:
log(a/b) = log(a) - log(b)
d/dx log(f(x)) = f'(x)/f(x)
이런 식들을 이용해서 유도하면 쉽게 나옵니다.
Y가 원핫 벡터이냐(첫 번째 word 선택)에 따라 식이 조금 다르게 유도됩니다.
모든 시점에 대해 일반화
이걸 모든 t 시점에 대해서 고려하면:
∂J/∂V = Σₜ ∂Jₜ/∂V
동일한 gradient를 모든 시점에서 구한 다음에 다 더한다는 얘기입니다.
은닉층에 대한 Gradient: 가장 복잡
V에 대해서도 하고, W에 대해서, U에 대해서 동일한 방식으로 gradient를 구하는데...
그중에서 가장 MLP와 다르고 우리가 좀 집중해서 봐야 될 부분은 은닉층에서의 미분입니다.
왜 복잡한가?
은닉층은 특별합니다:
- 출력층으로부터 gradient를 받음
- 다음 시점으로부터도 gradient를 받음
양방향으로부터 gradient를 얻어서 업데이트하는 유일한 부분이기 때문에, 은닉층에 대한 미분을 좀 더 면밀하게 살펴볼 필요가 있습니다.

마지막 시점: 단순
마지막 시점 hₜ의 gradient는 간단합니다:
∂J/∂hₜ = Vᵀ · (∂J/∂oₜ)
여기서만 계산되니까 어렵지 않죠.
중간 시점: 두 곳에서 온다
그런데 t-1 같은 경우는:
- t-1번째 자기 현재 시점의 출력값에도 영향
- 다음 시점(t)의 출력값에도 영향
따라서 term이 두 개가 생깁니다:
∂J/∂hₜ₋₁ = (현재 시점 출력) + (다음 시점으로부터)
= Vᵀ·(∂J/∂oₜ₋₁) + Wᵀ·D·(∂J/∂hₜ)
여기서 D는 hyperbolic tan의 미분값을 diagonal 부분에만 취한 행렬입니다.

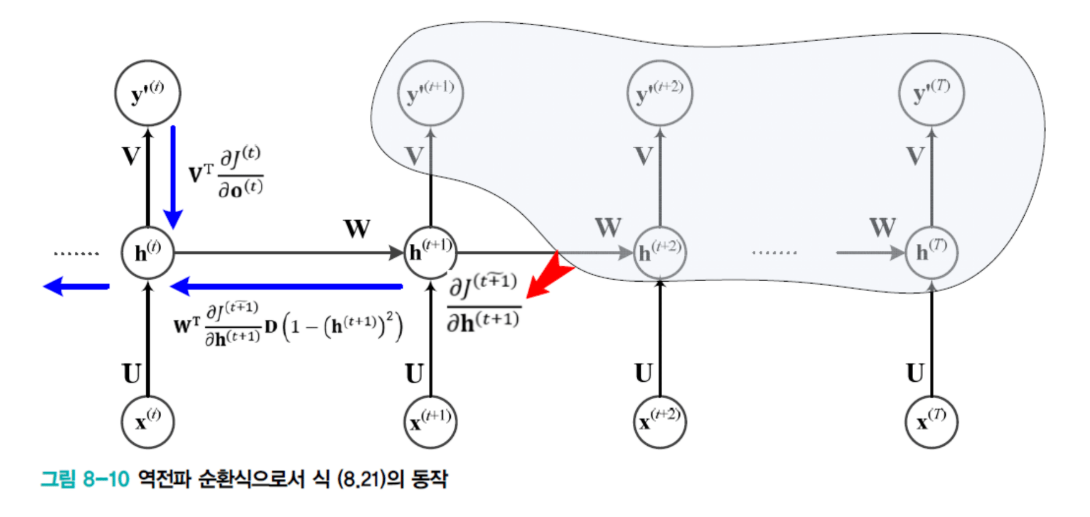
BPTT의 핵심: 끝에서 앞으로
그림으로 나타내면:
맨 끝 hidden node의 gradient:
↓
여기로부터 계산 (단순)
중간 hidden node의 gradient:
↓ (출력으로부터)
↓ (다음 시점으로부터)
두 gradient가 합쳐짐
앞쪽으로 계속 전파...
BPTT는 맨 끝에서부터 시점에 따라서, 또 레이어에 따라서 끝에서부터 앞으로 한 칸씩 이동하면서 gradient가 합쳐지는 형태로 계산됩니다.
이게 BPTT의 핵심입니다.

LSTM: 메모리라는 혁명
핵심 아이디어: 기억 장치
LSTM의 풀네임은 Long Short-Term Memory, 장단기 메모리입니다.
핵심 아이디어는 단순합니다: 메모리를 두자.
메모리가 뭐죠? 기억 장치입니다. 중요한 "길동"이라는 정보를 메모리에 담아뒀다가, 마지막에 "쉬었다"가 나올 때 "길동"이라는 정보를 꺼내서 "길동은 쉬었다"를 예측하는 겁니다.
메모리 안에는 장기 기억(long-term)과 단기 기억(short-term)을 둘 다 저장할 수 있도록 합니다.
메모리의 두 가지 오퍼레이션
컴퓨터 메모리를 생각해보세요. 메모리가 가진 가장 중요한 두 가지 동작이 뭔가요?
**Read(읽기)**와 **Write(쓰기)**입니다.
LSTM도 마찬가지입니다. 메모리를 구현하기 위해 **게이트(gate)**를 도입했습니다.
게이트는 뭘까요? 메모리에 read를 할지, write를 할지를 결정하는 신호를 만들어내는 컴포넌트입니다.
작동 예시
예를 들어볼까요?
- Write 신호 발동: "길동은"이라는 정보가 메모리에 쏙 들어갑니다
- Write 신호 차단: "길동은" 정보가 메모리에 저장된 채로 훼손되지 않고 유지됩니다
- 쓸데없는 말들 통과: "어제", "친구랑", "소풍" 같은 정보들이 지나갑니다
- Read 신호 발동: "쉬기로"라는 중요한 정보가 들어올 때, 메모리에서 "길동은"을 꺼냅니다
- 정보 결합: "길동은" + "쉬기로"가 합쳐져서 출력으로 전달됩니다
이렇게 Write와 Read를 게이팅 기법으로 적응적으로(adaptively) 제어합니다.
"적응적"이라는 말의 의미: 입력 단어에 따라서 어떤 애들은 메모리에 집어넣고, 어떤 애들은 튕겨내고, 어떤 때는 메모리에서 읽어서 출력하고, 어떤 때는 메모리를 거의 읽지 않고 출력하도록 만드는 거죠.

RNN vs LSTM: 구조적 차이
기본 골격은 동일
RNN과 LSTM은 사실 동일한 구조를 가지고 있습니다.
둘 다:
- 입력층
- 은닉층
- 출력층
차이는 은닉 노드를 취급하는 방식입니다.

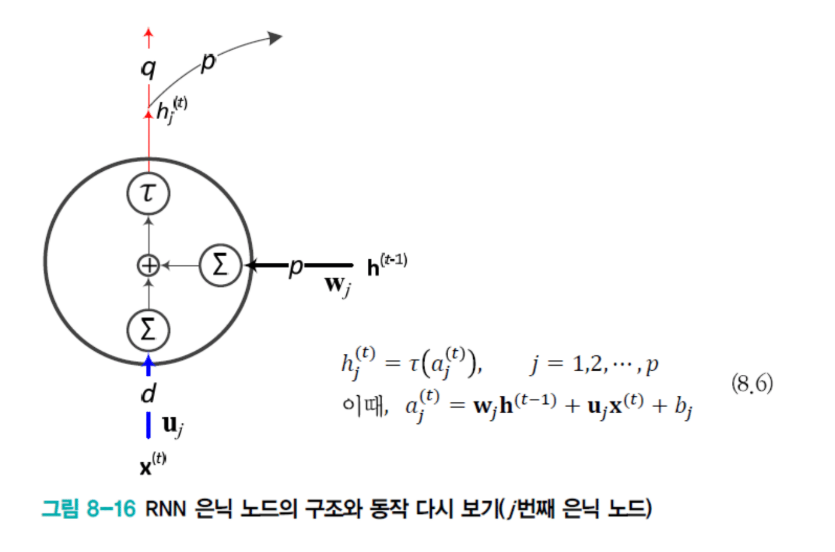
RNN: 무조건 섞인다
RNN은 은닉 노드가 항상 이전 은닉 노드 값과 현재 입력이 필연적으로 더해져야 합니다.
h_t = f(U·x_t + W·h_{t-1} + b)
중요한 정보든 아니든 무조건 똑같이 곱해지고 더해집니다. 아무리 중요한 정보가 들어있어도 똑같이 변하기 때문에 희석될 수밖에 없는 구조죠.
LSTM: 선택적으로 저장
LSTM은 은닉 노드를 메모리 블록으로 만들고, 이걸 입력 게이트와 출력 게이트로 감쌉니다.
현재 입력: U·x_t + W·h_{t-1}
이 값이 메모리 블록으로 들어가려고 할 때:
- 입력 게이트 값이 1이면: 메모리 블록 안에 쏙 들어감
- 입력 게이트 값이 0이면: 값이 튕겨져 나감 (0 곱하기 x = 0)
출력도 마찬가지:
- 출력 게이트 값이 1이면: 메모리에서 값이 나감
- 출력 게이트 값이 0이면: 어떤 값도 나가지 않음
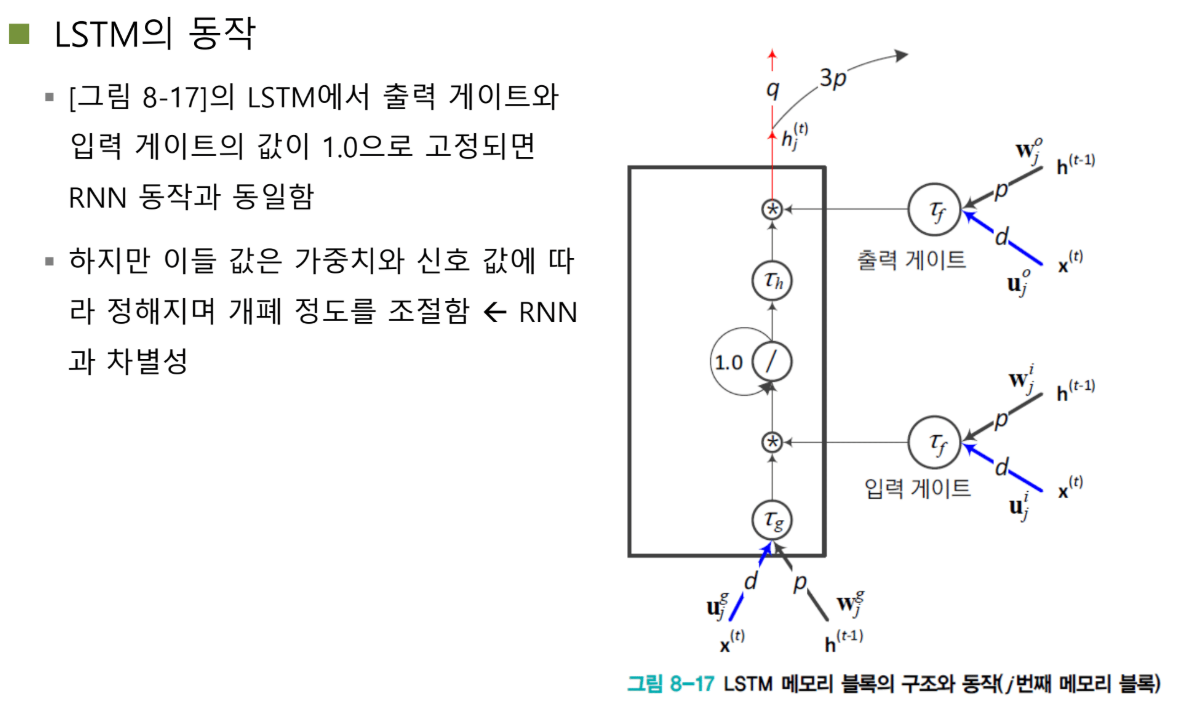
핵심: X가 세 곳에 쓰인다
중요한 부분을 봅시다.
입력 X가:
- 원래 입력으로 사용 (은닉 노드 계산)
- 입력 게이트에도 X 사용 (게이트 제어)
- 출력 게이트에도 X 사용 (게이트 제어)
입력 단어가 중요한지 안 한지를 판단하기 위한 가중치 벡터들이 입력 게이트와 출력 게이트에 존재합니다. 입력 값이 중요한 값인지 아닌지를, 게이트에서 알아차려서 문을 열지 말지 결정하는 거죠.
두 번째 중요한 점: H 값도 모든 곳에 들어갑니다.
입력: U·x_t + W·h_{t-1}
입력 게이트: U_i·x_t + W_i·h_{t-1}
출력 게이트: U_o·x_t + W_o·h_{t-1}
입력 게이트와 출력 게이트는 현재 x와 이전 h 값을 가지고 열지 말지를 결정하는 레이어입니다.
LSTM의 수식: 완전히 동일한 구조
세 개의 동일한 연산
잘 보세요. 굉장히 중요한 통찰입니다.
입력단, 입력 게이트, 출력 게이트는 사실 완전히 동일한 operation을 수행합니다.
모두:
- X를 입력으로 받고
- h_{t-1}을 입력으로 받고
- U와 W를 곱함
딱 봤을 때 "어? 이름만 다르고 똑같이 생긴 거 아니야?"라는 생각이 들죠. 맞습니다! 똑같은 연산을 해요.
두 가지 차이점
차이점 1: 가중치가 다르다
입력단에서 사용하는 U와 입력 게이트에서 사용하는 U_i와 출력 게이트에서 사용하는 U_o는 당연히 다른 가중치입니다.
학습을 통해 값을 결정하지만, 다른 값이 학습될 확률이 높습니다.
차이점 2: Activation 함수가 다르다
이게 핵심입니다!
입력단: tanh (Hyperbolic Tangent)
- 출력 범위: -1에서 1
- 은닉 벡터의 값으로 사용
게이트들: sigmoid
- 출력 범위: 0에서 1
- 문을 열고 닫는 역할
왜 sigmoid일까요? 게이트는 열고 닫는 역할을 하니까 0에서 1 사이의 값이 필요한 거죠.
Hyperbolic tan: ───┐ ┌───
└─────┘
-1 0 1
Sigmoid: ┌──────────
│
──┘
0 1
게이팅의 의미:
- 1에 가까우면: 통과! (중요한 정보)
- 0에 가까우면: 차단! (쓸데없는 정보)
출력도 마찬가지입니다:
- 1에 가까우면: 출력하는 데 중요하니까 통과
- 0에 가까우면: 지금은 출력에 중요하지 않으니 차단
파라미터 3배 증가
LSTM은 메모리 구조를 구현하기 위해 네트워크 크기를 크게 늘렸습니다.
원래: U, W, V LSTM: U, U_i, U_o / W, W_i, W_o / V
3배로 늘어났습니다!
솔직히 제가 생각했을 때는 게이팅을 하는 데 좀 많은 파라미터를 사용하지 않았나 싶어요. 과한 경향이 있습니다.
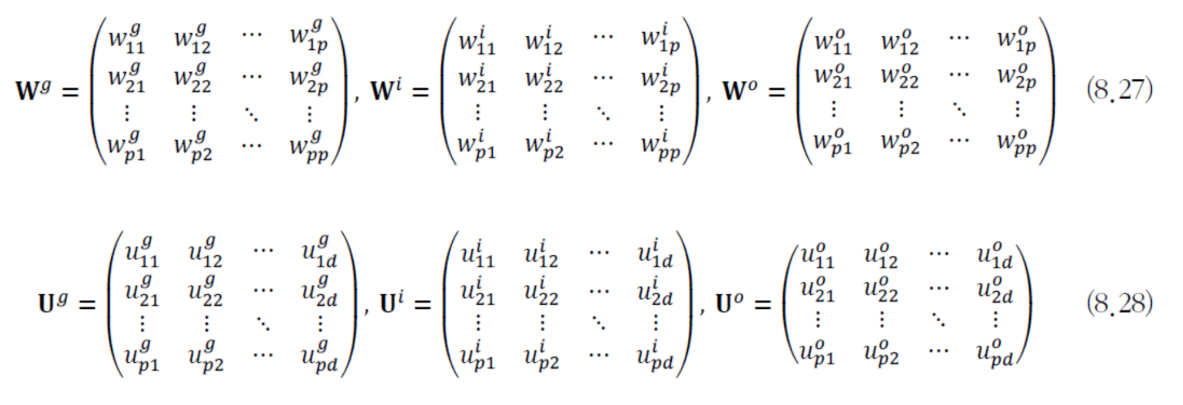
메모리 셀의 작동
S: 메모리 안의 벡터
S는 메모리 안에 들어있는 값입니다.
메모리 안에 들어있는 벡터는 자기 자신을 계속 반복해서 갱신합니다. 디지털 논리 회로 시간에 배운 플립플롭을 기억하시나요?
플립플롭은:
- 0 또는 1로 만들거나
- 클락이 들어오면 자기 값을 계속 반복해서 갱신
플립플롭과 같은 의미입니다. 자기 값을 계속 갱신하는 부분이죠.

입력 게이팅
새로운 입력 G가 들어왔을 때, 게이팅 정도에 따라서 메모리 안의 값을 얼마나 덮어쓸지 결정합니다.
S_t = S_{t-1} + i_t ⊙ g_t
- i가 1이면: g가 기존 S와 완전히 동일한 비율로 더해짐
- i가 0이면: 현재 들어온 입력은 제거됨
"방금 너가 입력한 word는 예측하는 데 전혀 중요한 word가 아니야."
이런 word들은 메모리에 못 들어오게 차단시켜버립니다.
지속적 저장
덜 중요한 word들은 계속 i가 0에 가까운 값을 가지겠죠. 그래서 맨 처음에 "철수는"이라는 정보가 메모리 안에서 다른 정보와 희석되지 않고 계속 반복을 통해 갱신되는 겁니다.
출력 게이팅
출력할 때도 마찬가지로 개폐 신호를 가지고 얼마나 출력을 많이 할지 결정합니다.
h_t = o_t ⊙ tanh(S_t)
- o가 1이면: 현재 S를 전체 다 출력
- o가 0이면: S 값을 전혀 고려하지 않고 0 벡터
이 두 게이트가:
- 메모리에 있는 값을 얼마나 저장할지
- 메모리 안의 값으로부터 얼마나 현재 h 벡터를 반영해서 만들지
이 두 가지를 조절합니다.


LSTM의 한계: 오버피팅
한 학생이 날카로운 질문을 했습니다.
"길동은과 쉬기로 작정하였다가 중요한 정보를 학습을 통해서 알아낸다고 했는데, 만약 훈련 집합에 '철수는'이라는 단어가 없는 상태로 훈련이 진행됐으면, '철수는'이 들어와도 중요하다고 일반화가 될까요?"
정확한 지적입니다.
일반화가 안 되면 오버피팅이 나서 트레이닝 집합에서만 중요한 단어를 진짜 중요하다고 보겠죠.
충분히 이런 고민이 될 수 있습니다. "얘가 우리 사람 마음대로 철수는 열어주고 다른 건 닫았다가 쉬었는데에서 다시 또 열어주고... 그렇게 잘 작동할까? 거기서 한 치의 오차라도 생기면 어떻게 될까?"
파라미터가 너무 많다
LSTM은 가중치가 엄청나게 많습니다. U와 W 매트릭스가 굉장히 큰 매트릭스인데, 얘를 3배를 써버립니다.
결국 파라미터가 너무 많아서 오버피팅에 사실 굉장히 취약합니다.
제가 LSTM을 몇 번 써봤는데, 이게 하이퍼파라미터를 조금만 바꾸면 학습이 잘 안 된다든지 하는 일들이 너무 잘 일어나더라고요.
LSTM을 학습하는 것 자체가 생각보다 굉장히 쉽지 않은 일이라는 걸 경험했습니다.
훈련 집합에서는 중요하다고 하는데 테스트 집합에서 조금 바꿨는데 전혀 안 중요하다고 해서 그냥 닫아버리는 것도 많이 발생할 수 있습니다. 충분히 가능한 얘기죠.
망각 게이트: 메모리 리셋
메모리에 리셋 버튼이 없다?
지금까지 봤더니 조금 미흡한 부분이 있습니다.
컴퓨터를 생각해보세요. 컴퓨터를 딱 킬 때 메모리를 리셋하잖아요? 리셋한 다음에 부트 코드 올리고 이렇게 쫙 올라가는데...
Read와 Write는 있는데, Reset이 없어!
그래서 리셋 버튼까지 만든 것이 **망각 게이트(Forget Gate)**입니다.
언제 필요한가?
두 문장이 있습니다:
[문장 1: .... .... ....] → Y1 예측
[문장 2: .... .... ....] → Y2 예측
첫 번째 문장과 두 번째 문장이 아무런 관련이 없습니다.
첫 번째 문장만으로도 충분히 Y1 예측하고, 두 번째 문장 시작부터 받아도 Y2 예측하는 데 아무런 문제가 없는 경우...
앞에 있던 정보를 다 날리고 싶을 수 있습니다. 메모리를 플러싱(flushing), 비우고 싶은 거죠.
망각 게이트가 발동해서 메모리 안의 값을 0으로 만들어버립니다.
망각 게이트의 구현
망각 게이트도 마찬가지로 x와 h_{t-1}을 둘 다 입력으로 받습니다.
f_t = σ(U_f·x_t + W_f·h_{t-1})
그래서 W 매트릭스가 하나 더 늘어납니다.
입력단 / 입력 게이트 / 출력 게이트 / 망각 게이트
U U_i U_o U_f
W W_i W_o W_f
4개씩! 게이트를 추가할 때마다 모델 크기가 훨씬 더 크게 늘어납니다.

작동 방식
S_t = f_t ⊙ S_{t-1} + i_t ⊙ g_t
망각 게이트의 출력값(0에서 1 사이)이 S에 element-wise로 곱해집니다.
- f가 0이 되면: 앞에 있는 값은 다 사라지고
- 새로운 정보가 메모리에 가득 참
학생 질문: 미래를 어떻게 알고 지우나?
"T 시점의 X를 보고 망각을 한다고 이해했는데, 이후 시점에 전 정보가 중요해질 수도 있지 않나요?"
그럴 수 있죠!
이후 시점에 얘가 중요할지 안 할지는 학습을 통해 결정되는 겁니다. 학습 과정에서 그 모든 게 다 잘 반영되기를 간절히 바라는 거죠.
실제로 그럴진 아닐지도 모릅니다. 나중에 사용될 수 있는 정보인데 그냥 지워버릴 수도 있어요. 당연히 일어날 수 있는 일이죠.
GRU: 천재의 개선
한국인 연구자의 통찰
우리나라 연구자 중에 자연어 처리 대가분이 계십니다. 조경현 교수님.
그분이 LSTM을 연구하다가 "이거 조금 약간 개선하면 좋겠는데"라고 해서 LSTM을 **GRU(Gated Recurrent Unit)**라는 모델로 개선했어요.
그분이 포닥을 할 때 LSTM 수식을 뚫어지게 보다가 이 부분에서 약간 이상함을 느낀 거예요.
무엇이 이상했나?
S_t = f_t ⊙ S_{t-1} + i_t ⊙ g_t
──────────── ─────────
망각 게이트 입력 게이트
이 부분이 괜찮은 방법인가?
생각해보세요:
- 입력이 많이 들어오면 → 앞에 있는 걸 잊어버리는 게 맞죠?
- 입력이 작게 들어오면 → 앞에 있는 걸 유지하는 게 맞죠?
둘 다 까먹어버리거나 둘 다 높게 할 필요가 없는 거예요!
두 개가 서로 반비례 관계에 있다는 걸 생각하신 겁니다.
GRU의 개선
S_t = (1 - i_t) ⊙ S_{t-1} + i_t ⊙ g_t
입력 게이트 하나로 망각 게이트와 입력 게이트를 대신합니다!
- 입력이 많이 들어와 (i가 크면) → 그만큼 지워 (1-i가 작아짐)
- 입력이 안 들어와 (i가 작으면) → 유지해 (1-i가 커짐)
놀라운 결과
게이트 하나를 줄였습니다. U와 W 매트릭스 하나를 날린 거니까 굉장히 줄인 건데...
이렇게 했더니:
- ✓ 모델 사이즈 감소
- ✓ 오버피팅 감소
- ✓ 속도 향상
- ✓ 성능은 비슷하거나 더 좋음
그래서 조경현 교수님이 GRU로 일약 스타가 되셨죠. 현재는 뉴욕대학교에서 교편을 잡고 계십니다.
이걸 생각해낼 수 있다니! 정말 연구자적 자질이 출중하신 분입니다.
Peephole: 내부 상태 활용
한 단계 더
Peephole 연결이라는 것도 있습니다.
아이디어: 블록의 내부 상태 S에 따라서 게이트를 제어하자.
f_t = σ(U_f·x_t + W_f·h_{t-1} + P_f·S_{t-1})
i_t = σ(U_i·x_t + W_i·h_{t-1} + P_i·S_{t-1})
o_t = σ(U_o·x_t + W_o·h_{t-1} + P_o·S_t)
어떤 특정 단어가 발생해서 S에 들어가면, 이 특정 단어에 따라서:
- 망각 게이트를 자동으로 열지
- 출력 게이트를 열지
- 입력 게이트를 닫을지 열지
를 결정하도록 하는 게 Peephole의 기능입니다.
결국 파라미터를 더 써서 성능을 높이겠다는 아이디어죠.
제가 알기로는 일반적으로 많이 사용하지는 않는 것 같습니다.
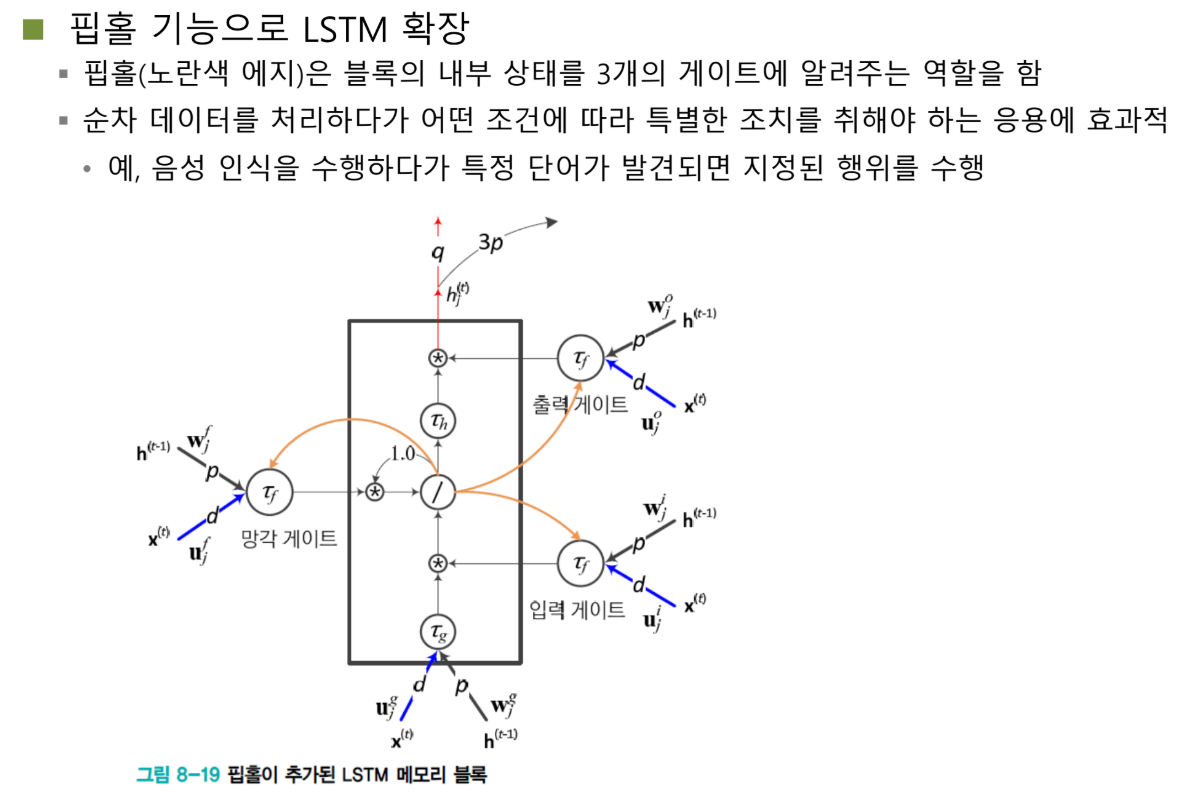
양방향 RNN: 미래도 보자
문맥은 양방향이다
문장을 봅시다:
"지시(指示)"
"거지(乞食)"
끝에 어떤 단어가 들어있냐에 따라 "지시"가 될 수도 있고 "거지"가 될 수도 있습니다.
"행색"이라는 말과 "거지"는 잘 어울리지만, "행색"과 "지시"는 안 어울리잖아요?
내가 특정 순서의 단어 문맥을 파악할 때는 앞에 있는 정보도 중요할 수 있지만, 뒤에 있는 정보를 같이 고려할 경우 더 정확하게 이 단어가 의미하는 것을 캡처할 수 있습니다.
그래서 문맥 의존성을 양방향으로 주자. Forward만 주지 말고 Backward도 같이 주자!
이렇게 나온 것이 Bidirectional RNN입니다.
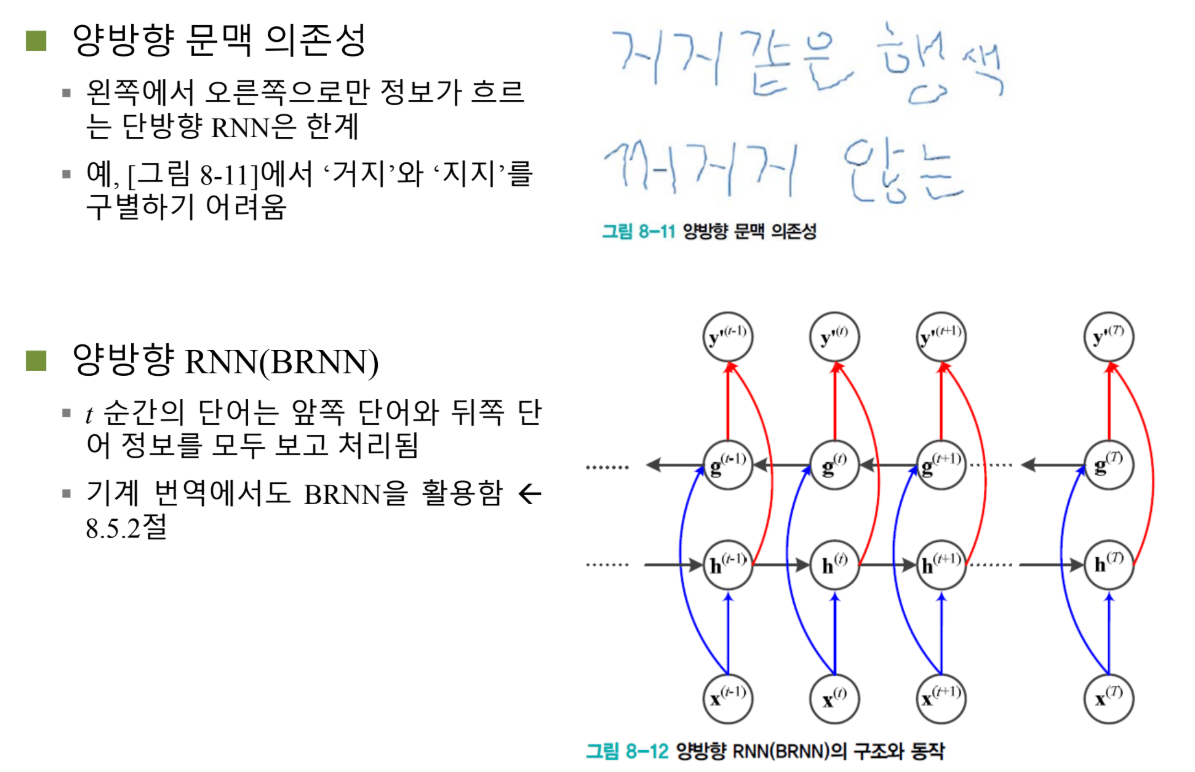
작동 방식
간단합니다:
1단계: Forward Pass
x_1 → h_1 → h_2 → h_3 → ... → h_T
맨 처음에 x를 쭉 집어넣어서 h를 계산합니다. 이전 x와 이전 h만 가지고 현재 h를 계산하는 거죠.
2단계: Backward Pass
x_T → g_T → g_{T-1} → ... → g_1
끝에서부터 g를 계산합니다. g는 역방향 은닉 노드 값입니다.
- Forward: X_1이 가장 먼저 영향
- Backward: X_T가 가장 먼저 영향
3단계: 결합
y_t = V·[h_t, g_t]
최종 출력은 정방향으로 얻어진 은닉 노드 값과 역방향으로 얻어진 은닉 노드 값을 합쳐서 만듭니다.
양방향으로 문맥 의존성을 고려해서 더 풍요로운 정보를 얻겠다는 시도입니다.
현대의 게이팅: NeurIPS Best Paper
게이팅은 과거의 유물인가?
여러분이 생각할 수 있습니다: "이거 너무 옛날 방법 아니야?"
아닙니다! 게이팅 기법은 지금도 엄청나게 활발하게 사용되고 있습니다.
게이팅을 잘 해서 올해 NeurIPS에서 Best Paper Award를 받은 논문이 있습니다.
제가 이 얘기를 하는 이유는, 현재 우리가 배우고 있는 게 옛날 방법 같지만 거기에 들어있는 intuition은 아직도 굉장히 유용하게 사용될 수 있고, 여러분들이 이런 것들을 잘 기억하고 계셨다가 나중에 어떤 중요한 문제를 만났을 때 활용하실 수 있기 때문입니다.
NeurIPS란?
NeurIPS는 머신러닝 분야에서 가장 좋은 학회입니다. 세계적인 모든 논문을 다 모았을 때 손가락 안에 드는 학회예요.
1위 Nature, 2위 Science 하면, 8~9위에 NeurIPS가 있을 정도로 엄청난 임팩트를 자랑하는 ML 분야 최고 학회입니다.
Gated Attention
그 학회에서 Best Paper를 받은 논문: Gated Attention
우리가 항상 강조하는 개념들:
- Nonlinearity: Activation 함수를 왜 씁니까? Nonlinearity 때문
- Sparsity: L1 norm을 왜 씁니까? Sparsity를 위해
Sparse하면 할수록 좋다. Nonlinear하면 할수록 좋다.
이 논문의 핵심: Attention에 Sparsity를 자유롭게 주는 게이팅 방법
Attention Mechanism 복습
Attention Mechanism은 뭐냐? 입력되는 단어들을 다 집어넣어보고:
- "철수는"과 "쉬었다"가 서로 연결되어 있는지
- "그녀는 ... 릴리가 ..." → "릴리"와 "그녀"가 같은 사람인지
이런 **관계 정보(relation)**를 얻어낼 수 있는 레이어가 Attention 레이어입니다.
Scaled Dot-Product Attention을 쓰는데, Query, Key, Value라는 게 있어요. 하나의 토큰을 가지고 각각 만들어내는 것인데...
간단한 아이디어
거기에 게이팅을 다 달아본 겁니다!
Sigmoid 함수를 달아봤어요:
- Query에 게이팅
- Key에 게이팅
- Value에 게이팅
- Attention 끝난 다음 마지막에도 게이팅
토큰을 입력으로 넣어서 0에서 1 사이의 값이 나오도록 게이팅을 걸어본 거죠.
놀라운 효과
G1 (마지막 출력에 게이팅):
- Perplexity가 0.265만큼 감소 (성능 향상)
- Loss가 학습 중에 막 튀는 현상이 사라짐
- 더 낮은 좋은 로컬 미니멈으로 수렴
한마디로 출력에다 곱하기만 해도 튀는 녀석이 사라지면서 더 좋은 곳으로 수렴한다는 게 이 논문의 contribution입니다.
왜 Best Paper가 되었나?
컨트리뷰션이 굉장히 간단하죠? "게이팅을 여기다 달았다."
그런데 Best Paper까지 된 이유는, 왜 이런 게이트를 다는 게 중요한지에 대한 근본적인 문제를 처음으로 발견했기 때문입니다.
Attention Sink 문제
발견된 근본 문제
Attention Sink이라는 문제가 있었습니다.
Attention Mechanism은 어떤 단어가 서로 다른 단어랑 얼마나 긴밀하게 관련되어 있는지를 결정하기 위해 Softmax를 씁니다.
Softmax를 쓰면:
- 가장 관련 있는 토큰: 큰 값
- 나머지 토큰: 0에 가까운 attention score
그런데 문제는 뭐냐?
가장 첫 번째 토큰을 키로 넣었을 때, 대부분의 쿼리와 가장 많은 attention을 가지고 있었습니다.
왜 문제인가?
첫 번째 토큰은 사실 아무 의미 없는 토큰입니다. 그냥 문장 시작 플래그를 가지고 있는 거예요.
그런데 그런 토큰을 모든 다른 토큰들이 attention했다는 말의 의미는 무엇일까요?
Softmax의 한계
특정 단어가 실제로 문장 안의 다른 단어랑 attention될 일이 별로 없어요. 아무 관련이 없는 단어야. 그냥 상관없는 단어.
그런데 그런 것들도 Softmax를 통과하면 어떤 토큰이랑은 반드시 attention이 되어야 됩니다. 합이 1이 되는 관점에서요.
쉽게 말해서 Softmax 자체가 무조건 하나 선택해야 한다는 거죠.
그러다 보니까 가장 첫 번째 있는 토큰이 제일 만만해서, 아무 이유 없이 - 진짜 attention 관계가 있어서 그런 게 아니라 - 그냥 첫 번째 토큰이라서 다른 토큰들이 다 얘를 선택한 겁니다.
악순환
이런 식으로 해서 첫 번째 토큰, 이 키에 엄청난 값이 몰려듭니다.
Attention score가 0.4처럼 굉장히 큰 값이 첫 번째 토큰에 몰려 있고, 이 문제로 인해서:
- 이 큰 값이 한 번 발생
- 이 큰 값이 전체 네트워크에 더 큰 값을 양산
- 출력 loss가 탁 튀면서
- 학습을 저해
Gating의 해결
이 큰 값 튀는 곳에다가 게이팅을 걸어줘서 이 큰 값이 몰리지 않도록 했습니다.
다시 학습을 했을 때:
- ✓ Attention이 골고루 분포
- ✓ 첫 번째 토큰의 attention score가 굉장히 낮아짐
- ✓ 학습이 안정화
논문의 실용적 조언
Practical Recommendations
논문의 요약, 베스트 실천 방법:
1. Apply element-wise SDPA Gating (G1)
- G1에다가 게이팅을 그냥 걸어라
2. Increase Learning Rate
- 과거에는 learning rate를 작게 쓸 수밖에 없었던 이유가 attention sink 때문
- 엄청나게 큰 값이 양산되어서 gradient 폭발을 막기 위해 어쩔 수 없이 작은 learning rate 사용
- 이제는 큰 값이 한 토큰에 모이지 않고 attention score가 골고루 분포
- 전체 값이 안정화
- Learning rate를 더 크게 해도 gradient 폭발 없이 더 좋은 곳으로 빠르게 수렴
이게 이 논문이 가지고 있는 의지입니다.
계산량은?
학생 질문: "게이트 때문에 attention 계산량이나 그런 거 비교가 어떻게 되나요?"
워낙 attention 쪽이 복잡하다 보니까, 게이팅하는 게 x만 입력을 받거든요. 한 토큰만 입력으로 받아서 가중치랑 게이팅을 합니다.
계산량 증가는 거의 없습니다.
에필로그: 게이팅의 교훈
왜 이 얘기를 했나?
제가 이 말씀을 드린 이유는:
지금도 게이팅 방법이 많이 활용되고 있고, 여러분들도 이 intuition을 잘 기억하셨다가 나중에 뭔가 모델도 만들고 하는데 값이 막 튀어서 학습이 너무 불안정한 경우, 한번 게이팅 방법을 써보는 것도 좋지 않을까 하는 마음에서 말씀드렸습니다.
간단하지만 아카데믹
이 논문은 굉장히 간단하지만 사실은 굉장히 아카데믹합니다.
굉장히 중요한 문제를 잘 파고들어가서, 그 문제를 아주 간단한 방법으로 해결한 명작이다. 저는 그렇게 생각합니다.
게이트 구현: if문이 아니다
학생 질문: "게이트는 그러면 코드로 if-else문으로 해도 되지 않나요?"
안 됩니다! if-else문이면 미분이 안 됩니다. 게이트가 학습이 안 되죠.
if-else문이 아니라 sigmoid를 씁니다.
gate = σ(Wx + b)
이렇게 생긴 거죠. 마이너스 무한대에서 무한대인 값을 0에서 1 사이의 값으로 맵핑해주는 거예요.
- 큰 값이 되면 → 1에 가깝게 게이트를 열어주고
- 음수가 나오면 → 게이트를 닫아주고
게이트가 꼭 반드시 100% 열고 100% 닫는 건 아닙니다. 반쯤 열 수도 있고 반쯤 닫을 수도 있습니다.
미분 가능하기 때문에 backpropagation으로 학습할 수 있습니다.
마무리: 메모리에서 Attention까지
핵심 통찰들
LSTM의 교훈:
- 메모리는 Read/Write/Reset으로 구현
- 게이팅으로 선택적 정보 저장
- 대신 파라미터 3~4배 증가, 오버피팅 위험
GRU의 천재성:
- 입력과 망각의 반비례 관계 발견
- 게이트 하나 제거로 성능 향상
- 간단한 통찰이 큰 개선을 만듦
Bidirectional RNN:
- 문맥은 양방향이다
- Forward + Backward = 풍부한 정보
현대의 게이팅:
- Attention Sink 문제 해결
- 학습 안정화
- 여전히 활발히 연구되는 기법
영원한 원칙
게이팅의 본질은 변하지 않습니다:
- 선택적 정보 흐름: 중요한 건 통과, 불필요한 건 차단
- 0과 1 사이: Sigmoid로 미분 가능하게 구현
- 학습 가능: Backpropagation으로 자동 조정
LSTM부터 현대 Transformer까지, 이 원칙은 계속 살아있습니다.
여러분이 나중에 모델을 만들 때, 값이 튀거나 학습이 불안정하면 게이팅을 떠올리세요. 아직도 유효한 강력한 도구입니다.