희소 코딩과 오토인코더
복습: PCA와 ICA
지난 시간 내용을 간단히 정리하고 시작합니다.
분산은 어디서 재나요? Z축에서 잽니다. Projection된 공간에서의 샘플 분산을 의미해요. 그리고 찾아진 축들이 서로 orthogonal하다는 점도 중요합니다.
라그랑주 승수법은 언제 사용하나요? 목적함수를 최적화할 때 등식 조건이 있을 때 씁니다. 최적해에서 목적함수와 조건식의 gradient가 평행해지는 성질을 이용하는 거죠.
수식으로 쓰면:
L = f + λ(g - c)
f가 최적화하려는 것, g가 조건이에요. 미분해서 쓸 거니까 c는 적분상수라 안 적어도 상관없습니다.
ICA 복습
**독립 성분 분석(ICA)**은 블라인드 원음 분리 문제를 풉니다. 보이스톡할 때 여러분 목소리와 카페 시끌시끌한 배경음을 분리하는 것처럼요.
X에서 Z로 가는 W가 무수히 많아서 과소조건 문제입니다. 해가 너무 많죠. 이럴 때 유일한 방법은 조건을 추가해서 해를 특정하는 겁니다.
추가 조건 두 가지:
- 독립성: 피아노 소리와 바이올린 소리는 서로 독립적으로 발생. 피아노가 바이올린에 영향을 주지 않음.
- 비가우시안: 소리 분포가 가우시안이 아니라 중심이 뾰족한 분포. 첨도(kurtosis)를 최대화해서 W를 구합니다.
PCA vs ICA:
PCA ICA
| 가정 | 가우시안 | 비가우시안 |
| 모멘트 | 2차 (분산) | 4차 (첨도) |
| 축 관계 | 반드시 직교 | 직교 아니어도 됨 |
| 용도 | 차원 축소 | 원음 분리 |
ICA는 축이 90도일 필요가 없어서 자유도가 더 높습니다. 표현력 관점에서 더 자유롭죠. 그래서 일반적으로 ICA 성능이 더 좋습니다.
희소 코딩: 학습으로 좋은 축 찾기
PCA, ICA는 미분으로 빠르게 축을 찾았습니다. 희소 코딩은 점진적인 gradient 방식의 학습으로 좋은 축을 찾습니다. 그것도 희소(sparse)한 방식으로요.
신호는 기저 벡터의 선형 결합
이 세상의 모든 신호는 기저 벡터와 계수의 선형 결합으로 표현할 수 있습니다.
푸리에 변환을 예로 들어볼게요. 구형파 신호가 있다고 합시다.
첫 번째 basis: ~~~~ (낮은 주파수)
두 번째 basis: ~~~~ (더 높은 주파수)
세 번째 basis: ~~~~ (더더 높은 주파수)
...
이 기저 함수들에 가중치를 곱해서 더하면:
구형파 = 0.8×(첫 번째) + (-2)×(두 번째) + 1.5×(세 번째) + 4×(네 번째) + ...
0.8, -2, 1.5, 4 같은 값들이 '계수(coefficient)'이고, 각각의 사인/코사인 함수가 '기저 함수(basis function)'입니다.
푸리에 변환의 기저 함수는 고정되어 있습니다. 사인, 코사인 함수죠. 학습으로 바꿀 수 없어요.
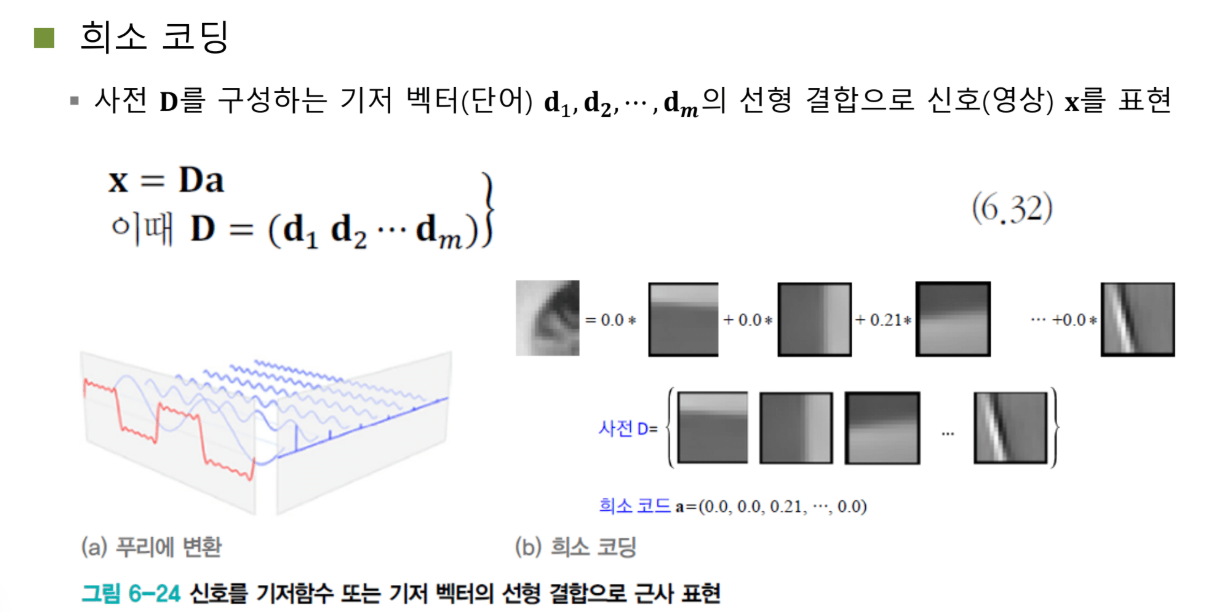
희소 코딩의 아이디어
희소 코딩은 푸리에 변환을 학습 가능한 기저 벡터로 확장합니다.
X = D × A
- D (Dictionary): 기저 벡터들을 모아놓은 행렬. 첫 번째 열이 첫 번째 basis, 두 번째 열이 두 번째 basis...
- A (Coefficient): 각 기저 벡터의 가중치
핵심 조건: A가 희소(sparse)해야 한다.
A = [0, 0.21, 0, 0, 0, 0.3, 0, 0, 0.5, 0, 0, ...]
대부분이 0이고 몇 개만 0이 아닌 값을 가집니다.
이게 무슨 말이냐면, 엄청나게 많은 기저 벡터 패턴들 중에서 몇 개의 패턴만 가지고 신호를 복원하겠다는 거예요.
예시
물결무늬 이미지가 있습니다. 딕셔너리에 64개의 기저 벡터가 있어요.
이 물결무늬를 표현하는 데 64개 중 36번, 42번, 63번 세 개만 사용합니다.
A = [0, 0, ..., 0.8, ..., 0.3, ..., 0.5, 0, ...]
(36번) (42번) (63번)
이 세 개 기저 벡터의 선형 결합으로 원래 물결무늬를 만들어내는 거죠.
Overcomplete 딕셔너리
신호가 16차원이라고 합시다. 16개 기저 벡터면 100% 복원 가능합니다.
그런데 희소 코딩에서는 64개, 256개처럼 훨씬 많은 기저 벡터를 만듭니다. 이걸 overcomplete하다고 해요.
왜 그럴까요?
16개를 16개 기저로 보내면 A 벡터가 sparse하지 않습니다. 대부분 값이 0이 아니에요.
하지만 16개를 256개로 보내면 그중 2~3개만 골라서 복원할 수 있습니다. 더 sparse하게 만들 수 있는 거죠.
Sparsity가 왜 중요한가?
여러분이 궁금해하실 겁니다. A 벡터에 0이 많은 게 왜 중요할까요? 왜 굳이 2~3개만 써서 복원해야 할까요?
첫째, 압축률이 좋아집니다.
0이 많다는 건 엔트로피가 낮다는 뜻입니다. 압축하기 쉬워요.
딕셔너리를 서버랑 스마트폰에 둘 다 저장해둡니다. 영상을 보낼 때 A 벡터만 전송하면 됩니다. A가 대부분 0이니까 "36번 0.8, 42번 0.3, 63번 0.5"만 보내면 되죠. 엄청난 압축률입니다.
둘째, 신호가 선명해집니다.
여러 기저 벡터를 섞으면 섞을수록 신호가 평균화됩니다. 블러해지죠. 스파스하게 선택하면 선명한 신호가 복원됩니다.
셋째, 노이즈가 제거됩니다.
노이즈는 고주파입니다. 지글지글한 고주파를 복원하려면 엄청나게 많은 기저 벡터가 필요해요. 스파스 조건 때문에 그런 것들은 선택될 확률이 낮아집니다. 자연스럽게 노이즈가 제거되는 거죠.
희소 코딩의 최적화
수식으로 쓰면:

첫 번째 항: 딕셔너리에서 스파스한 기저를 골라서 X를 복원하라 두 번째 항: A는 스파스해야 함 (대부분 0이어야 함)
문제는 D도 unknown이고 A도 unknown이라는 겁니다. 모름 × 모름 = X.
가우시안 믹스처랑 같은 상황이에요. EM 알고리즘처럼 풀어야 합니다.
D 고정 → A 최적화
A 고정 → D 최적화
반복
D를 좋은 값으로 초기화하는 게 중요합니다. 보통 푸리에 변환의 삼각함수로 초기화한 다음 점점 업데이트해요.
추론할 때도 어렵습니다. D만 주어지고 새로운 X가 들어오면 sparse한 A를 찾아야 하는데, 이것도 반복을 통해 refinement해야 해요. 추론 시간이 길었던 방법입니다.
희소 코딩의 흥망성쇠
한 시대를 풍미했던 거대한 연구 흐름이었습니다.
5~10년 동안 모든 태스크를 스파스 코딩으로 풀었어요. 회귀도, 분류도, 압축도. 엄청나게 복잡한 Hierarchical Dictionary 구조까지 진화했습니다.
그러다가 딥러닝이 나오면서 싹 정리됐습니다.
공룡의 멸종과 같았어요. 공룡이 더 강력해지는 방향으로 진화했다면(몸집 키우기, 이빨 날카롭게), 딥러닝은 완전히 새로운 패러다임(뇌의 진화)으로 등장한 거죠.
지금도 sparsity라는 개념은 중요합니다. 0을 많이 만든다는 아이디어는 딥러닝에서도 유용해요. 하지만 스파스 코딩 자체는 더 이상 주류가 아닙니다.
오토인코더: 뉴럴넷으로 인코딩/디코딩
드디어 스파스 코딩 패러다임을 넘어서 신경망으로 인코딩과 디코딩을 해봅니다.
기본 구조

'오토(Auto)'는 자기 자신을 의미합니다. 자기 자신(X)을 입력으로 넣어서 자기 자신(X)을 출력으로 받는 구조예요.
X → [Encoder f] → H (또는 Z) → [Decoder g] → X̂
- Encoder: X를 H로 매핑하는 뉴럴넷 f
- Decoder: H를 다시 X로 매핑하는 뉴럴넷 g
목적함수:
minimize ||X - X̂||²
X를 그대로 복원하는 인코딩-디코딩 네트워크를 학습하는 겁니다.
조건이 없다
오토인코더가 강력한 이유는 어떤 조건도 없다는 점입니다.
- ICA: 첨도가 뾰족해야 함
- PCA: 찾은 축들이 직교해야 함
- 오토인코더: 아무 조건 없음
학습으로 가장 좋은 표현을 찾습니다. 굉장히 flexible하게 representation을 만들어낼 수 있어요.
병목 구조
가장 중요한 설계는 **병목(bottleneck)**입니다.
X (65,000차원) → H (1,000차원) → X̂ (65,000차원)
65,000개를 집어넣는데 1,000개만 통과시켜야 해요. 그 1,000개로 다시 65,000개를 복원해야 합니다.
엄청난 병목이죠. 이 1,000차원 안에 가장 중요한 정보만 들어가게 됩니다. 덜 중요한 나머지 64,000차원의 정보는 필터링됩니다.
Z 공간에 뭐가 들어가나?
Z 안에 어떤 정보가 들어갈까요? 단순한 픽셀 값이 아닙니다.
의미론적으로 중요한 정보가 들어갑니다:
- 남자인지 여자인지
- 머리가 긴지 짧은지
- 피부색은 어떤지
- 안경을 꼈는지
Vector Arithmetic
Z를 조작하면 재미있는 일을 할 수 있습니다.
안경 낀 남자들의 이미지를 잔뜩 모아서 인코더에 통과시킵니다. 나온 Z들의 평균을 구해요. 이게 "평균화된 안경 낀 남자" 레이턴트입니다.
안경 안 낀 남자들도 마찬가지로 평균 Z를 구합니다.
안경 안 낀 여자들의 평균 Z도 구합니다.
그리고:
Z_안경낀여자 = Z_안경낀남자 - Z_안경안낀남자 + Z_안경안낀여자
이 Z를 디코더에 넣으면? 안경을 낀 여자가 생성됩니다!
이게 의미하는 건 뭘까요? Z 공간에 있는 값들이 의미론적으로 중요한 표현을 가지고 있다는 겁니다. 안경 유무, 성별 같은 특징들이 Z에 매핑되어 있어요.
단순 복사가 아닌 이유
가장 단순한 오토인코더는 W를 곱하고 W inverse를 곱하는 겁니다. 또는 identity matrix를 두 번. 정보 손실 0이죠.
하지만 그건 무의미합니다. identity로 매핑된 공간이 의미 있는 공간이 되지 않거든요.
의미 있는 표현을 얻으려면 규제 기법이 필요합니다.
병목 구조의 응용
특징 추출: Z가 핵심 정보를 담고 있으니까, X 대신 Z를 분류기에 넣어도 좋은 성능이 나옵니다. 65,000차원 대신 1,000차원으로 분류하는 거죠.
영상 압축: 유튜브 스트리밍. 서버에서 Z를 보내고 스마트폰에서 디코더로 X를 복원합니다.
시각화: Z를 2차원으로 만들면 데이터의 내재된 구조를 시각화할 수 있습니다.
다양한 구조
입력 < 은닉: 병목 구조 (일반적) 입력 = 은닉: 동일 구조 입력 > 은닉: 확장 구조
확장 구조도 쓸모가 있을까요?
네, GAN이 바로 그 구조입니다. 랜덤 노이즈 Z를 넣어서 이미지 X를 생성하죠. 오토인코더를 뒤집은 거예요.
이안 굿펠로우가 술집에서 친구들과 맥주를 마시다가 발견했다고 합니다. "오토인코더 뒤집어 버릴까?" 했더니 생성이 너무 잘 되더라고요.
다양한 오토인코더
Sparse Autoencoder
히든 레이어의 대부분 값을 0으로 만듭니다. 병목을 더 병목화해서 정보를 초고농축으로 압축하는 거죠.
Denoising Autoencoder
입력에 노이즈를 태웁니다. 원래 X를 복원하는 것도 어려운데, 노이즈까지 섞어서 복원하게 합니다.
콩쥐팥쥐에서 콩쥐한테 밭 갈고 물까지 채우라고 하는 것처럼, 어려운 일을 두 개 시키는 거예요.
네트워크가 두 개의 태스크를 동시에 풀면서 더 강력한 표현을 학습합니다. 실제로 이렇게 하면 레이턴트의 representation power가 확 올라갑니다.
핵심 컨셉: 초등학생에게 미적분을 가르치자. 역경을 극복하면서 더 좋은 표현력을 배우는 거죠.
Jigsaw Puzzle
이미지를 9등분해서 순서를 섞습니다. 원본 순서대로 복원하게 하는 거예요.
네트워크는 패치들 사이의 **관계(relation)**를 배워야 합니다. 머리 밑에는 턱선이 있어야 한다는 것처럼요. 훨씬 더 어려운 태스크를 풀면서 표현력이 좋아집니다.
Masked Autoencoder (MAE)
가장 최신 방법입니다. 2022년에 나왔어요.
퍼즐보다 더 어렵게 합니다. 아예 정보를 주지 않아요. 몇 개의 패치만 넣고 나머지를 전부 복원하게 합니다.
레이블 필요 없이 X만 있으면 됩니다. 일부 영역을 블랙아웃시키고 그 영역까지 복원하게 하면 표현력이 더 강해집니다.
현재 Self-Supervised Learning의 대세입니다. ChatGPT, Diffusion 이미지 생성, 비디오 생성... 최신 딥러닝 모델은 기본적으로 이런 마스크드 방법으로 먼저 학습한 다음 파인튜닝합니다.
Colorization
흑백 이미지를 넣고 컬러 이미지를 출력하게 합니다. 레이블 필요 없죠.
컬러를 입히려면 고차원적 인지 능력이 필요합니다. 나무는 초록색과 갈색, 하늘은 파란색... 어떤 사물 옆에 있을 때 다른 컬러를 가질 수 있다는 추론도 해야 해요.
난이도 조절의 중요성
더 어려운 태스크를 줄수록 좋은 건 아닙니다.
퍼즐 섞고 + 마스킹하고 + 노이즈까지 태우면? 네트워크가 학습 자체를 포기합니다. 표현이 굉장히 안 좋아져요.
적당한 난이도가 핵심입니다.
복습 질문
1. 희소 코딩의 핵심 아이디어
핵심: 신호를 기저 벡터와 계수의 선형 결합으로 표현하되, 계수 대부분이 0
수식: X = DA, where A is sparse
푸리에 변환과 차이: 푸리에는 고정된 삼각함수, 희소 코딩은 학습된 기저 벡터
Overcomplete 딕셔너리: 입력 차원보다 훨씬 많은 기저 벡터 → 더 sparse하게 선택 가능
2. Sparsity의 세 가지 장점
- 압축률 향상: 0이 많으면 엔트로피 낮음. 딕셔너리 공유하고 A만 전송
- 선명한 복원: 여러 기저 섞으면 블러해짐. 적게 선택하면 선명
- 노이즈 제거: 고주파 노이즈는 많은 기저 필요 → sparse 조건 때문에 자연스럽게 제거
3. 오토인코더의 병목 구조
구조: 입력 >> 은닉 << 출력 (예: 65,000 → 1,000 → 65,000)
왜 중요?
- 1,000차원을 통과하려면 가장 중요한 정보만 선택됨
- 덜 중요한 정보는 필터링
- 의미론적 특징이 Z에 인코딩됨 (성별, 안경 유무 등)
Vector Arithmetic: Z 공간에서 덧셈/뺄셈으로 새로운 이미지 생성 가능
4. Denoising Autoencoder의 원리
방법: 입력에 노이즈 추가 후 원본 복원
원리: 두 가지 어려운 태스크 동시 수행
- 원본 복원
- 노이즈 제거
결과: 더 강력한 representation 학습
비유: 콩쥐에게 밭 갈고 물까지 채우라고 시키기
5. Masked Autoencoder (MAE)
방법: 입력의 일부만 제공, 마스킹된 부분까지 복원
특징:
- 레이블 불필요 (Self-Supervised)
- 2022년 등장, 현재 대세
- ChatGPT, Diffusion 등의 기반 기술
주의: 너무 어려우면 학습 포기 → 적절한 난이도 조절 필요
6. PCA, ICA, 희소 코딩, 오토인코더 비교
PCA ICA 희소 코딩 오토인코더
| 기저 | 고유벡터 | 독립 성분 | 학습된 딕셔너리 | 뉴럴넷 |
| 조건 | 직교 | 비가우시안 | 스파스 | 없음 |
| 최적화 | 미분 | 첨도 최대화 | EM 방식 | 역전파 |
| 특징 | 분산 최대화 | 원음 분리 | 압축 효율 | 유연한 표현 |