시간이 흐르는 데이터를 이해하는 법: 순환 신경망 이야기
프롤로그: 사진에서 동영상으로
지금까지 우리가 배운 신경망은 모두 정지된 순간을 다뤘습니다. 컨볼루션 신경망으로 이미지를 분류할 때, 그건 1분 37초에 찍은 영상, 어느 한 순간 T 시점의 스냅샷이었죠. 마치 사진 한 장을 보고 "이건 고양이야, 저건 강아지야"라고 판단하는 것처럼요.
그런데 세상에는 시간이 흐르는 데이터가 훨씬 많습니다. 심장 박동 신호, 주식 시세, 음성, 문장, 유전자 염기서열... 이 모든 것들은 시간에 따라 변화합니다. t-1 시점의 값, t 시점의 값, t+1 시점의 값이 연속적으로 이어지며 의미를 만들어냅니다. 우리는 이런 데이터를 '순차 데이터(sequential data)'라고 부릅니다.
사진과 동영상의 차이를 생각해보세요. 사진은 한 순간을 담지만, 동영상은 시간의 흐름을 담습니다. 데이터 양의 차이도 그 정도입니다. 정적 데이터와 순차 데이터는 사진 한 장과 유튜브 동영상 하나만큼의 차이가 납니다.
순차 데이터를 다루는 모델의 진화
순차 데이터를 처리하기 위해 세 가지 주요 모델이 차례로 개발되었습니다.
'RNN (Recurrent Neural Network)'이 가장 먼저 나왔습니다. 순환 신경망이라고 부르죠. 순환한다는 게 무슨 뜻일까요? 과거의 정보가 다시 돌아와서 현재에 영향을 준다는 의미입니다. 이 기본적인 아이디어가 순차 데이터 처리의 문을 열었습니다.
하지만 RNN에는 치명적인 약점이 있었습니다. 정보가 시간이 지나면서 점점 희석된다는 거죠. 마치 속삭임 게임처럼, 첫 번째 사람이 말한 내용이 열 번째 사람에게 전달될 때쯤이면 거의 알아들을 수 없게 되는 것처럼요.
이 문제를 해결하기 위해 'LSTM (Long Short-Term Memory)'이 등장했습니다. 장단기 메모리라는 이름에서 알 수 있듯, 중요한 정보를 메모리에 저장했다가 필요할 때 꺼내 쓰는 메커니즘을 도입했습니다. 선별적 기억 능력이라고 할 수 있죠.
그리고 현재는 Transformer의 시대입니다. 여러분이 사용하는 ChatGPT, 이미지 생성 AI, 모든 대형 언어 모델이 Transformer 기반입니다. 언어, 비전, 비디오, 강화학습, 로봇... 모든 분야가 Transformer로 통합되고 있습니다. Multimodal LLM, Vision-Language LLM처럼 여러 양식을 통합하는 방향으로 계속 발전하고 있죠.
얀 르쿤의 틀린 예언
2022년쯤 유명한 AI 연구자 얀 르쿤이 트위터에 이렇게 선언했습니다: "Transformer는 사라질 것이다. 계산 복잡도가 너무 높아서 결국 감당할 수 없을 거다."
그의 근거는 타당했습니다. Transformer의 Attention Mechanism은 입력 토큰 개수의 제곱에 비례해서 계산량이 증가하거든요. 토큰이 두 배가 되면 계산량은 네 배가 됩니다.
실제로는 어떻게 되었을까요? Transformer를 위협할 모델들이 나오긴 했습니다. 맘바(Mamba), 리포머(Reformer) 같은 것들이죠. 하지만 전혀 위협적이지 않았습니다. 대신 Transformer의 Attention Mechanism을 경량화하는 방향으로 발전하고 있어요. Low-rank로 표현하거나 선형으로 만들어서 O(n²) 복잡도를 줄이는 거죠.
당분간 Transformer의 아성을 위협할 모델은 없을 것 같습니다.
그런데 왜 RNN을 배우나요?
"Transformer가 짱인데 왜 RNN을 배워야 하죠?"라고 물을 수 있습니다. 답은 간단합니다. Transformer를 제대로 이해하려면 RNN과 LSTM을 반드시 알아야 하기 때문입니다.
건물의 꼭대기 층을 이해하려면 기초부터 올라가야 하는 것처럼요. RNN과 LSTM은 Transformer의 기반이 되는 아이디어들을 담고 있습니다. 이 강의에서는 그 기초를 다지는 것이고, Transformer 자체는 고급 딥러닝이나 자연어 처리 수업에서 자세히 다룹니다.
순차 데이터는 어디에나 있다
순차 데이터의 가장 중요한 특징은 가변 길이입니다. 샘플마다 길이가 다릅니다.
ChatGPT를 사용할 때를 생각해보세요. 어떤 사람은 "그건 왜 그래?"라고 짧게 묻습니다. 다른 사람은 "A는 B고 C는 D인데, A가 D가 되기 위해서는 블라블라블라..." 하며 장황하게 설명하죠. 답변도 마찬가지입니다. "네, 맞습니다"처럼 간단할 수도 있고, 300단어짜리 긴 설명일 수도 있습니다.
이런 가변 길이를 자연스럽게 수용할 수 있어야 순차 데이터를 제대로 다룰 수 있습니다.
우리 주변의 순차 데이터들
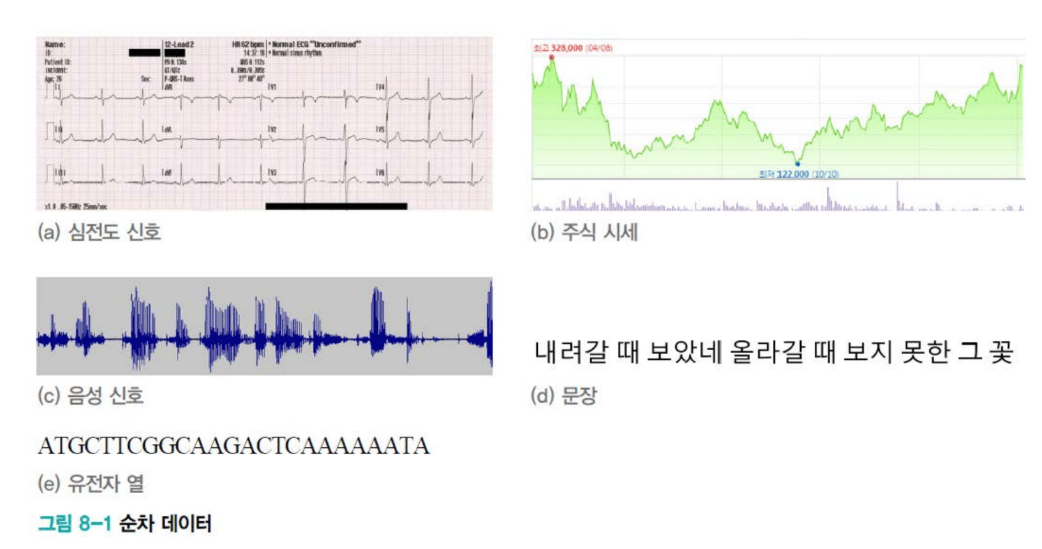
심전도 신호를 봅시다. 심장이 뛸 때마다 전기적 신호가 발생합니다. 이걸 초당 100번 샘플링하고 2분간 측정하면 어떻게 될까요? 총 12,000개의 측정값이 나옵니다. X = [X₁, X₂, ..., X₁₂,₀₀₀]. 이 신호의 패턴을 분석하면 부정맥을 진단할 수 있습니다.
주식 시세는 또 어떤가요? 코스피 값이 시간에 따라 오르락내리락합니다. 각 시점의 가격이 순차적으로 이어지며 추세를 만들죠. 이 패턴을 분석하면 언제 사고 팔아야 하는지, 지금 코스피 4천이 적정선인지 판단할 수 있습니다.
음성 신호도 순차 데이터입니다. 소리의 파형이 시간에 따라 변합니다. 이걸 디지털로 샘플링한 게 음성 데이터죠. 음성 인식 시스템은 이 순차 데이터를 텍스트로 변환합니다.
문장은 가장 대표적인 순차 데이터입니다. 단어들이 순서대로 나열되어 의미를 만듭니다. "내가 밥을 먹었다"와 "밥이 나를 먹었다"는 완전히 다른 의미죠.
유전자 염기서열도 순차 데이터입니다. A, T, G, C라는 네 가지 염기가 어떤 순서로 배열되느냐에 따라 생명체의 특성이 결정됩니다. 유전자 가위 기술도 이 순서를 조작하는 겁니다.
심지어 필기체 숫자도 순차 데이터로 볼 수 있습니다. 숫자를 그냥 2차원 이미지로 볼 수도 있지만, 사람이 펜으로 그리는 스트로크(획)의 과정으로 볼 수도 있어요. 어떤 방향으로 획을 긋느냐, 어떤 순서로 그리느냐를 벡터로 표현하면 순차 데이터가 됩니다. 경우에 따라서는 완성된 이미지를 보는 것보다 그리는 과정을 보는 게 더 정확할 수 있죠.
세상에는 엄청나게 많은 순차 데이터가 있습니다. 이걸 잘 처리할 수 있으면 정적 데이터만 다룰 때보다 훨씬 더 많은 일을 할 수 있습니다.
벡터의 벡터: 순차 데이터의 표현
순차 데이터는 **벡터의 벡터(vector of vectors)**로 표현됩니다.
X = [X₁, X₂, X₃, ..., Xₜ]
X라는 샘플 벡터가 있는데, 그 안에 또 다른 벡터들(X₁, X₂, ...)이 들어있는 겁니다. 각 시점마다 하나씩요.
생각해보면 데이터 양이 엄청나다는 걸 알 수 있습니다. 정적 데이터는 벡터 하나인데, 순차 데이터는 그 벡터가 시간 축을 따라 수백, 수천 개씩 이어지니까요. 계산량도 당연히 훨씬 많이 필요합니다.
텍스트를 숫자로: 표현 방법의 진화
컴퓨터는 문자를 이해하지 못합니다. 숫자만 이해하죠. 그렇다면 "April is the cruelest month"라는 문장을 어떻게 숫자로 표현할까요? 이 문제를 해결하기 위한 방법들이 차례로 진화해왔습니다.
1. 사전(Dictionary): 빈도수 세기
가장 전통적인 방법은 사전을 만드는 겁니다. 모든 단어가 몇 번 나왔는지 세는 거죠. Histogram이나 Multinomial distribution이라고도 합니다.
April: 7번 출현
is: 8번 출현
the: 15번 출현
cruelest: 3번 출현
month: 5번 출현
역사적으로 유명한 예가 있습니다. 조라(Cho)라는 분이 영어-불어 번역 논문에서 가장 빈도가 높은 3만 개 단어를 사전으로 구축했어요. 3만 차원의 histogram이죠. 각 단어마다 빈도수가 쭉 나와 있는 겁니다.
2. Bag of Words: 단어를 자루에 담기
조금 더 나아가면 Bag of Words(단어 가방)입니다. 이름이 재미있죠? 단어를 커다란 자루에 집어넣고 막 뒤섞는다고 생각하면 됩니다. 레고 블록을 상자에 쏟아붓는 것처럼요.
순서는 없습니다. 그냥 빈도수만 세서 M차원 벡터로 만듭니다(M = 단어 개수).
장점은 엄청난 압축입니다. 천 페이지짜리 책이 있다고 해봅시다. 이 책에 등장하는 단어가 3천 개뿐이라면? 천 페이지의 모든 내용을 3천 차원 벡터 하나로 표현할 수 있습니다. 굉장히 compact하죠.
이게 어디에 쓰일까요? 정보 검색입니다. 논문 하나가 들어왔는데 이게 컴퓨터 과학 논문인지 생물학 논문인지 모르겠다면? 단어들을 Bag of Words로 histogram을 만든 다음, 각 분야의 대표 단어 histogram과 비교하는 겁니다. 컴퓨터 과학 분야 단어 빈도수와 더 유사하면 CS 논문인 거죠.
간단하고 차원도 낮으니까 검색에 딱 좋습니다.
하지만 치명적인 단점이 있습니다. 바로 순서 정보를 완전히 잃는다는 거예요.
생각해보세요. 단어는 순서를 가지고 배열됩니다. 주어, 동사, 목적어 순서가 있죠. "the"는 보통 맨 앞에 나오고, "is" 앞에는 "she"나 "he" 같은 주어가 있을 확률이 높습니다.
그런데 Bag of Words는 이 모든 순서를 무시하고 단어를 자루에 쏟아넣어버립니다. 그 결과 "April is the cruelest month"와 "the cruelest month is April"이 똑같은 벡터가 되어버립니다. 시간성 정보가 완전히 희석되는 거죠.
순차 데이터의 핵심은 순서인데, 그걸 표현할 수 없으니 기계학습에는 부적절합니다.
3. One-hot Encoding: 하나만 1, 나머지는 0
그래서 나온 게 One-hot Encoding(원핫 인코딩)입니다.
분류 문제에서 클래스를 표현하던 방법을 떠올려보세요. 사람은 [1,0,0], 차는 [0,1,0], 강아지는 [0,0,1]처럼 하나만 1이고 나머지는 다 0인 벡터로 만들었죠. 단어도 똑같이 합니다.
April: [1, 0, 0, 0, 0, ...]
is: [0, 1, 0, 0, 0, ...]
the: [0, 0, 1, 0, 0, ...]
cruelest:[0, 0, 0, 1, 0, ...]
month: [0, 0, 0, 0, 1, ...]
장점이 두 가지 있습니다.
첫째, 순서를 표현할 수 있습니다. 이 벡터들을 순서대로 쭉 모아놓으면 순차 정보가 보존되거든요.
둘째, 각 단어를 명확하게 구분합니다. 각 벡터가 서로 **직교(orthogonal)**합니다. 두 벡터를 내적하면 0이 나와요. 90도 각도를 이루고 있다는 뜻이죠. 각 단어가 완전히 독립적으로 표현됩니다.
그런데 문제가 심각합니다.
문제 1: 차원 폭발
영국인이 일상생활에서 쓰는 단어는 약 3천 개 정도랍니다. 이 정도면 문서를 읽고 일하는 데 아무 지장이 없습니다.
그런데 셰익스피어는 달랐습니다. 1만~2만 개의 단어를 알고 있었고, 그 단어들을 시의적절하게 써서 불후의 명작을 남겼죠.
셰익스피어 작품을 원핫 인코딩하면 어떻게 될까요? 단어가 2만 개니까, 한 단어를 표현하는 데 2만 차원 벡터가 필요합니다.
메모리 낭비가 어마어마합니다. 한 단어 표현하는 데 2만 개 숫자가 필요하다니!
문제 2: 유사도를 측정할 수 없다
세상의 단어들은 서로 관계가 있습니다. "she"와 "he"는 비슷한 단어죠. "good"과 "bad"는 반대 개념입니다. 이런 관계를 유사도로 표현하면 좋을 텐데요.
원핫 벡터는 모두 직교합니다. 어떤 두 단어를 내적해도 0이 나옵니다. 모든 단어가 똑같이 멀리 떨어져 있다는 뜻이죠.
그래서 단어 간의 유사도를 전혀 측정할 수 없습니다. 모든 단어가 동등하게 무관하게 표현되는 겁니다.
문제 3: 너무 Sparse해서 학습이 안 된다
이건 한 학생이 정확하게 지적해준 문제입니다. "너무 sparse해서 학습이 어렵지 않나요?"
정확합니다! 굉장한 통찰력이에요.
생각해보세요. 2만 차원 벡터인데 그중 하나만 1이고 나머지 19,999개는 다 0입니다. 엄청나게 sparse하죠.
Backpropagation을 떠올려봅시다:
∂L/∂wᵢ = (앞에서 온 gradient) × xᵢ
문제는 x가 대부분 0이라는 겁니다. x의 값이 0이면 gradient도 0이 됩니다. 네트워크 안의 텐서들이 대부분 0으로 채워져 있으니, gradient 계산할 때도 대부분 0이 나옵니다.
결과는? Gradient vanishing이 굉장히 빨리 발생합니다. 학습 자체가 안 되는 거죠.
이건 논문에서 지적된 문제인데, 그 논문을 읽지 않고도 이걸 꿰뚫어 본 학생의 통찰력이 대단했습니다.
교훈: 너무 sparse한 데이터는 학습이 불가능합니다. 어느 정도 dense해야 합니다.
4. Word Embedding: 드디어 찾은 해답
차원 폭발, 유사도 측정 불가, 학습 불가... 이 모든 문제를 한 번에 해결한 게 Word Embedding(단어 임베딩)입니다.
아이디어는 이렇습니다:
X (sparse, 20,000차원)
↓
× E (임베딩 행렬)
↓
Z (dense, 600차원)
고차원 sparse 벡터를 저차원 dense 벡터로 선형 변환하는 겁니다.
핵심은 E가 학습으로 결정된다는 거예요. 이 Z를 실제 모델(번역 모델이든 뭐든)에 집어넣어서 학습할 때, backpropagation이 E까지 흘러들어갑니다. 그래서 E도 함께 학습되는 거죠.
일반적으로 X는 2만 차원인데 Z는 600차원 정도입니다. 차원이 확 줄어들죠. 그리고 X는 굉장히 sparse한데, Z는 별로 sparse하지 않습니다. Sparsity 조건을 주지 않고 학습하니까 값이 꽉꽉 차있는 dense한 형태가 됩니다.
놀라운 발견: 의미가 모인다
단어 임베딩을 하면 놀라운 일이 발생합니다.
비슷한 의미를 가진 단어들끼리 저절로 모입니다!
임베딩 공간을 시각화해보면 "the", "its", "itself" 같은 단어들이 가까이 모여 있어요. 비슷한 의미의 단어들이 클러스터를 형성하고, 상반된 의미의 단어들은 멀리 떨어집니다.
아무도 "이 단어들은 비슷해"라고 가르쳐주지 않았는데, 학습 과정에서 의미론적 유사성이 자동으로 캡처되는 겁니다.
모든 문제 해결
단어 임베딩이 해결한 것들:
- ✓ Sparsity 문제: Dense하게 표현
- ✓ 차원 축소: 2만 → 600차원
- ✓ 유사성 캡처: 의미적으로 비슷한 단어가 가까이
현재 표준: 모든 LLM 모델은 반드시 단어 임베딩을 거친 Z를 입력으로 사용합니다. 단어 임베딩 없이는 현대 NLP가 작동하지 않습니다.
순차 데이터의 세 가지 본질
순차 데이터를 제대로 처리하려면 세 가지를 반드시 갖춰야 합니다.
1. 순서는 생명이다
단어는 똑같고 순서만 바뀌었을 뿐인데 의미가 크게 훼손되는 경우가 있습니다.
비순차 데이터는 순서를 바꿔도 무방합니다. 미니배치를 만들 때 고양이-강아지 순서로 넣든 강아지-고양이 순서로 넣든 학습에 전혀 차이가 없어요.
순차 데이터는 다릅니다. 섞는 순간 심각한 문제가 발생합니다. 의미 자체가 바뀌거나 완전히 사라져버리죠.
2. 길이는 제각각이다
샘플마다 길이가 다릅니다. 어떤 사람은 prompt를 엄청 정교하게 길게 써요. 저 같은 사람은 굉장히 짧게 쓰는 편이고요.
이 가변 길이를 자연스럽게 수용할 수 있어야 합니다.
순환신경망은 이걸 어떻게 해결할까요? 층에 **순환 엣지(recurrent edge)**를 부여해서 입니다. 과거 정보를 다시 돌려받아 사용하는 구조 덕분에, 입력이 몇 개든 상관없이 처리할 수 있습니다.
3. 맥락이 모든 것이다
비순차 데이터에서는 **공분산(covariance)**으로 특징 간 의존성을 표현합니다. 키와 몸무게를 생각해보세요. 각각 자신의 분산이 있고, 두 특징 사이에 공분산(상관관계)이 있죠.
순차 데이터는 다릅니다. 하나의 시점에서 X₁, X₂, X₃가 뭐냐는 사실 그렇게 중요하지 않습니다.
대신 시간에 따라 값들이 어떻게 바뀌는지, 서로를 어떻게 연결시키는지가 훨씬 중요합니다. t-1 시점의 값이 t 시점에 어떤 영향을 주는지, t+1 시점과는 어떤 관계인지... 이런 시간적 연결 관계가 핵심입니다.
문맥 의존성의 예
문장을 봅시다:
"그녀는 점심때가 다 되어서야 ... (중간에 많은 단어들) ... 먹었는데"
여기서 중요한 건 "그녀는"과 "먹었는데"의 연결입니다.
X₁이 "그녀는"이고 X₂₀이 "먹었는데"라고 하면, 이 둘 사이에 수많은 단어가 끼어 있습니다. 하지만 의미를 제대로 파악하려면 이 둘을 연결해야 합니다.
이렇게 멀리 떨어진 단어들을 이어줄 수 있는 능력을 **장기 의존성(long-term dependency)**이라고 부릅니다.
LSTM의 해결책
LSTM은 이걸 어떻게 해결할까요?
- "그녀는"이라는 정보를 메모리에 저장합니다
- 중간에 많은 단어가 지나갑니다
- "먹었는데"가 나타나는 순간
- 메모리에서 "그녀는"를 꺼냅니다
- 두 정보를 결합해서 의미 있는 출력을 만듭니다
메모리와 게이팅 메커니즘. 이게 LSTM의 핵심입니다.
순환 신경망의 탄생
자, 이제 본격적으로 RNN을 봅시다.
MLP와 거의 비슷한데...
RNN은 사실 Multi-Layer Perceptron(MLP)과 굉장히 비슷합니다.
둘 다 이렇게 생겼어요:
- 입력층 (Input layer)
- 은닉층 (Hidden layer)
- 출력층 (Output layer)
가중치 행렬도 있습니다:
- U: X → H (입력을 은닉층으로)
- V: H → Y (은닉층을 출력으로)
여기까지는 완전히 똑같습니다.
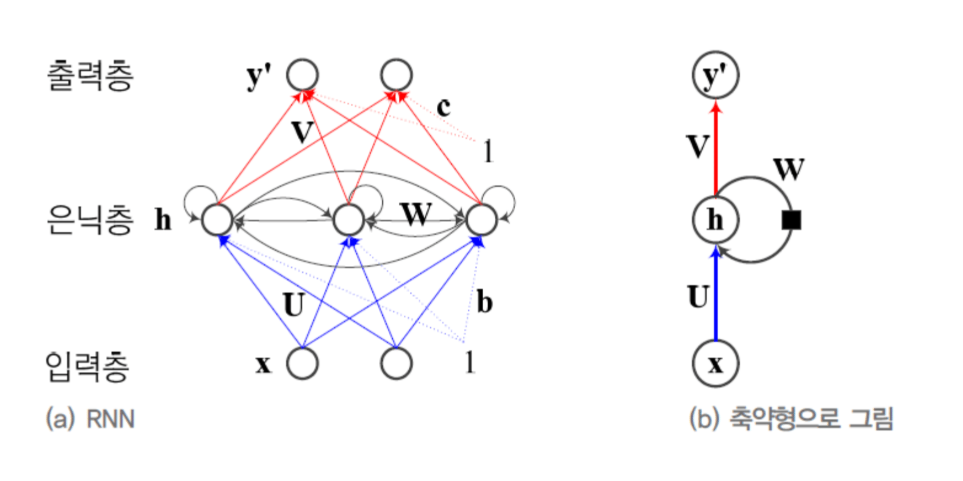
단 하나의 차이: W
차이는 딱 하나입니다. RNN에는 W라는 가중치 행렬이 하나 더 있습니다.
W ←┐
↓ │
X → U → H ─┤→ V → Y
W는 뭐 하는 녀석일까요?
은닉층의 H 값을 받아서 W를 곱한 다음, 다음 시점에 다시 은닉층으로 보냅니다. 과거의 은닉층 정보를 현재로 재활용하는 거죠.
이 **순환 엣지(recurrent edge)**가 RNN의 전부입니다. 이 하나의 아이디어가:
- 시간성
- 가변 길이
- 문맥 의존성
세 가지를 모두 처리할 수 있게 만들어줍니다.
MLP의 동작
먼저 MLP를 복습해봅시다:
X → U → H → V → Y
- 입력 X가 들어옵니다
- U와 곱해져서 은닉층 H가 만들어집니다
- H가 V와 곱해져서 출력 Y가 나옵니다
끝입니다. 깔끔하죠.
RNN의 동작
RNN은 조금 다릅니다:
W ←┐
↓ │
X → U → H → V → Y
↑
과거의 H
- 현재 입력 Xₜ가 들어옵니다
- U와 곱해집니다: U·Xₜ
- 그런데 여기서 끝이 아닙니다
- 과거 은닉층 Hₜ₋₁도 가져옵니다
- W와 곱해집니다: W·Hₜ₋₁
- 두 개를 더합니다: U·Xₜ + W·Hₜ₋₁
- 이게 새로운 은닉층 Hₜ가 됩니다
- Hₜ가 V와 곱해져서 출력 Yₜ가 나옵니다
수식으로 쓰면:
Hₜ = f(U·Xₜ + W·Hₜ₋₁ + b)
핵심: 과거 정보(W·Hₜ₋₁)가 현재 입력(U·Xₜ)에서 만들어질 은닉층 값을 변화시킵니다.
재귀적으로 펼쳐보기
시간을 따라가며 보면:
시점 1: H₁ = f(U·X₁ + W·H₀ + b)
시점 2: H₂ = f(U·X₂ + W·H₁ + b)
시점 3: H₃ = f(U·X₃ + W·H₂ + b)
...
시점 T: Hₜ = f(U·Xₜ + W·Hₜ₋₁ + b)
1번 시점에서 계산된 결과가 2번 시점으로 전달되고, 그 결과가 3번 시점으로 전달되고... 계속 반복됩니다.
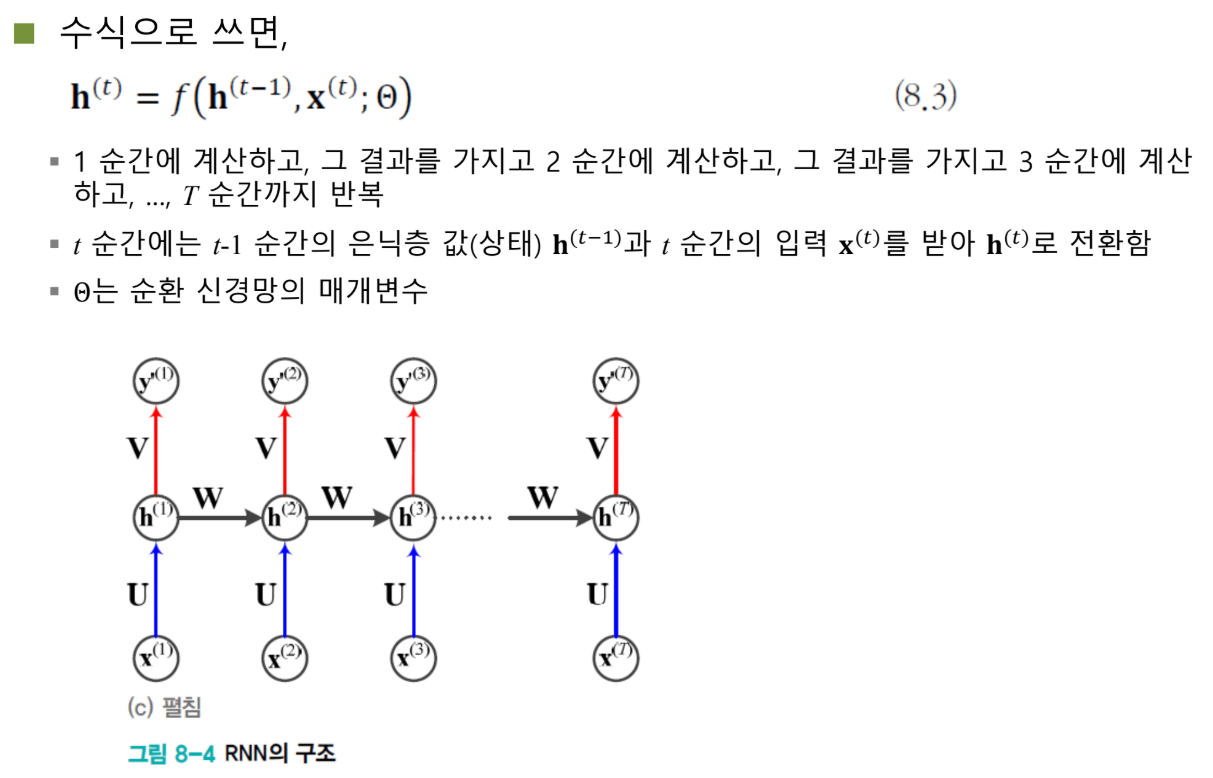
시간에 따라 펼쳐진 네트워크
RNN은 하나의 모델이지만, 시간 축을 따라 펼쳐서 볼 수 있습니다:
시점 1: X₁ → [U, W, V] → H₁ → Y₁
↓ W
시점 2: X₂ → [U, W, V] → H₂ → Y₂
↓ W
시점 3: X₃ → [U, W, V] → H₃ → Y₃
↓ W
...
시점 T: Xₜ → [U, W, V] → Hₜ → Yₜ
이렇게 보면 층을 여러 개 쌓은 심층 신경망처럼 보입니다. 은닉층과 출력층 2개밖에 없는 얕은 네트워크 같지만, 입력이 계속 들어가고 정보를 계속 갱신하니까 실질적으로는 깊은 네트워크인 셈이죠.
특징: 모든 층의 가중치가 동일합니다. 어느 시점이든 똑같은 U, W, V를 사용합니다.
파라미터 공유: 축복이자 저주
무엇을 공유하나?
RNN의 중요한 특징이 **매개변수 공유(parameter sharing)**입니다.
시점 1, 2, 3, ..., T 모두: 동일한 U, W, V
어떤 입력이 들어오든, 몇 번째 시점이든 항상 똑같은 가중치를 사용합니다.
파라미터 5개
RNN이 학습해야 할 파라미터는 총 5세트입니다:
- U (P × D): X(D차원)를 H(P차원)로
- W (P × P): H를 다음 H로 (자기 자신 차원)
- V (Q × P): H(P차원)를 Y(Q차원)로
- b (P차원): 은닉층 bias
- c (Q차원): 출력층 bias
RNN 학습의 목표: 훈련 데이터로 최적의 θ = {U, W, V, b, c}를 찾는 것
공유의 세 가지 축복
축복 1: 모델이 작아진다
만약 각 시점마다 다른 파라미터를 쓴다면?
U₁, W₁, V₁ (시점 1용)
U₂, W₂, V₂ (시점 2용)
U₃, W₃, V₃ (시점 3용)
...
Uₜ, Wₜ, Vₜ (시점 T용)
파라미터 개수가 시점 수에 비례해서 증가합니다. 엄청난 메모리가 필요하죠.
공유하면?
U, W, V (하나씩만!)
추정할 매개변수 수가 획기적으로 줄어듭니다. 이게 공유경제의 힘입니다. 물건 하나를 여러 사람이 돌려쓰니 물건을 여러 개 만들 필요가 없는 거죠.
축복 2: 가변 길이를 처리할 수 있다
입력 길이가 샘플마다 다릅니다. 어떤 문장은 5단어, 어떤 문장은 50단어입니다.
파라미터를 공유하니까 같은 U, W, V로 모든 길이를 처리할 수 있습니다. 길이가 짧으면 적게 쓰고, 길면 많이 쓰면 되니까요.
축복 3: 순서 변화에 강하다
"어제 이 책을 샀다"
"이 책을 어제 샀다"
"어제"의 위치가 바뀌었습니다. 하지만 똑같은 U, W, V를 사용하기 때문에 어느 정도 비슷한 출력을 냅니다.
매개변수가 같다는 건, 입력에 약간의 변화가 생겨도 적응적으로(adaptively) 동작한다는 뜻입니다. 순서 변화에 **강건(robust)**한 거죠.
공유의 두 가지 저주
하지만 공짜 점심은 없습니다.
저주 1: 병렬 처리가 안 된다
한 학생이 날카로운 질문을 했습니다: "GPU 병렬 처리가 안 되지 않나요?"
정확합니다!
GPU 병렬 처리가 가능하려면 각 스레드가 독립적이어야 합니다. 서로 의존성이 없어야 한다는 거죠.
RNN의 문제는:
Hₜ = f(U·Xₜ + W·Hₜ₋₁)
↑
과거 결과 필요!
시점 t를 계산하려면 시점 t-1의 결과가 반드시 필요합니다. 이전 계산이 끝나야 다음 계산을 할 수 있습니다.
Synchronization을 걸어야 하고, 병렬화가 매우 제한적입니다. 이게 RNN의 큰 약점 중 하나입니다.
저주 2: 정보가 희석된다
또 다른 학생이 통찰력 있는 질문을 했습니다: "U, W, V를 공유하면 과거 정보가 누적되면서 희석되는 거 아닌가요?"
정확합니다! 굉장한 통찰력입니다.
이게 RNN의 가장 치명적인 문제입니다. 자세히 봅시다.
정보 희석: RNN의 아킬레스건
희석의 메커니즘
같은 W를 계속 곱하면 어떤 일이 벌어질까요?
각 시점에서 과거와 현재가 반반(50:50)씩 기여한다고 가정해봅시다.
첫 입력의 기여도:
시점 1: 50%
시점 2: 50% × 50% = 25%
시점 3: 25% × 50% = 12.5%
시점 4: 12.5% × 50% = 6.25%
시점 5: 6.25% × 50% = 3.125%
...
기하급수적으로 감소합니다!
10번 후면 첫 입력은 거의 0%에 가까워집니다.
비유: 속삭임 게임
어렸을 때 속삭임 게임 해봤나요? 첫 번째 사람이 "오늘 날씨가 참 좋다"라고 말하면, 이게 차례차례 전달되면서 점점 왜곡됩니다. 열 번째 사람에게 도착할 때쯤이면 "온몸이 아프다" 같은 완전히 다른 말이 되어버리죠.
RNN의 정보 전달도 비슷합니다. 같은 W를 계속 곱하면서 원래 정보가 점점 희석됩니다.
결과: 최근 것만 기억한다
1. 장기 의존성 실패
"그녀는 ... (20개 단어) ... 먹었는데"
"그녀는"의 정보가 "먹었는데"까지 전달되지 못합니다. 중간에 희석되어 사라지거든요.
2. 최근 정보만 중요
마지막 몇 개 단어만 실제로 영향을 줍니다. 앞쪽 단어들은 거의 무시되는 거죠.
Gradient도 희석된다
학습할 때도 똑같은 문제가 발생합니다.
Loss → Hₜ → ... → H₃ → H₂ → H₁
↓ ↓ ↓ ↓
큰 gradient 중간 작음 아주 작음
Loss가 맨 끝에서 발생해서 역전파됩니다. 앞으로 갈수록 gradient vanishing이 일어납니다.
결과:
- X₁에 맞는 W, U: 거의 학습 안 됨
- Xₜ 근처의 W, U: 잘 학습됨
- 끝쪽 샘플들에만 집중
앞쪽 정보를 처리하는 능력이 제대로 발달하지 못하는 겁니다.
정보 희석은 RNN의 구조적 문제입니다. 그냥 희석되는 게 아니라 심각하게 희석됩니다.
해결책: LSTM의 메모리
이 문제를 해결하기 위해 LSTM이 탄생했습니다.
핵심 아이디어: 메모리 뱅크를 하나 만듭니다.
Memory Cell
├─ Forget Gate: 뭘 잊을까?
├─ Input Gate: 뭘 저장할까?
└─ Output Gate: 뭘 출력할까?
작동 방식:
- 선별적 저장: "그녀는"이라는 정보가 중요하다고 판단되면 메모리에 저장
- 선별적 제거: 중간에 중요하지 않은 정보는 메모리에서 빼냄
- 필요할 때 회상: "먹었는데"가 나타나면 메모리에서 "그녀는"을 꺼냄
- 정보 결합: "그녀는" + "먹었는데" → 의미 있는 출력
게이팅 메커니즘(gating mechanism): Gate(문)를 열었다 닫았다 하면서 정보를 선택적으로 제어합니다.
결과: 장기 의존성 해결! 50단어 이상 떨어진 단어도 연결할 수 있습니다.
LSTM의 M = Memory: Long Short-Term Memory, 장기·단기 메모리를 모두 처리합니다.
학습: 그래디언트를 모으고 한 방에!
그래디언트 누적
한 학생이 질문했습니다: "W, U, V를 공유하는데 gradient 갱신은 어떻게 하나요?"
답은 간단합니다. 각 시점에서 발생한 gradient를 모두 누적합니다.
시점 1에서: ∂L/∂V₁, ∂L/∂W₁, ∂L/∂U₁
시점 2에서: ∂L/∂V₂, ∂L/∂W₂, ∂L/∂U₂
시점 3에서: ∂L/∂V₃, ∂L/∂W₃, ∂L/∂U₃
...
이걸 다 모읍니다:
∂L/∂V = ∂L/∂V₁ + ∂L/∂V₂ + ... + ∂L/∂Vₜ
∂L/∂W = ∂L/∂W₁ + ∂L/∂W₂ + ... + ∂L/∂Wₜ
∂L/∂U = ∂L/∂U₁ + ∂L/∂U₂ + ... + ∂L/∂Uₜ
Gradient를 다 모은 다음에 한 방에 업데이트!
Backpropagation Through Time (BPTT)
이미 배운 backpropagation을 그대로 적용하면 됩니다.
펼쳐진 네트워크를 따라 역전파하면서:
- 각 지점에서 local gradient 계산
- Chain rule로 쭉 전파
- ∂L/∂V, ∂L/∂W, ∂L/∂U 모두 수집
- 같은 파라미터끼리 다 더하기
- 한 번에 업데이트
Loss도 각 시점마다
Y₁ → CrossEntropy → Loss₁
Y₂ → CrossEntropy → Loss₂
Y₃ → CrossEntropy → Loss₃
...
각 출력마다 loss를 계산합니다. 거기서 gradient가 발생해서 역전파되는 거죠.
끝에서 생성된 gradient는 맨 앞까지 전파되고, 중간에서 만들어진 gradient는 해당 지점까지만 영향을 줍니다.
다양한 입출력 구조
입력과 출력 개수가 다를 수 있다
T: 입력 개수
L: 출력 개수
이 둘이 항상 같을 필요는 없습니다.
Many-to-One: 여러 입력 → 한 출력
입력: "2000년 노벨평화상을 받은 사람은?"
출력: "김대중"
여러 단어를 입력받아 한 단어만 출력합니다.
Many-to-Many (불균형): 짧은 입력 → 긴 출력
입력: 짧은 prompt (몇 단어)
출력: 300단어 설명
ChatGPT가 이렇게 작동합니다.
Special Tokens
문장의 시작과 끝을 표시하는 특별한 토큰이 있습니다:
- <START> 또는 <SOS> (Start of Sequence)
- <END> 또는 <EOS> (End of Sequence)
<START> Y₁ Y₂ Y₃ ... Yₙ <END>
Training할 때: 모델이 언제 시작하고 끝나는지 학습합니다.
Inference할 때: <END> 토큰이 나올 때까지 계속 생성하고, 사용자에게는 <START>와 <END>를 빼고 중간 부분만 보여줍니다.
Transformer vs RNN: 계산 복잡도 전쟁
Transformer의 O(T²) 문제
Transformer의 Attention Mechanism은 엄청난 계산량을 요구합니다.
토큰: [I, am, Sam, <PAD>] (T=4개)
각 토큰: 2차원 벡터
Query(Q): 4×2 행렬
Key(K): 2×4 행렬
Attention Score = Q × K = (4×2) × (2×4) = 4×4 행렬
토큰이 4개면 4×4 행렬을 계산합니다.
토큰이 8개로 늘어나면?
8×8 행렬
계산량: 16 → 64 (4배!)
일반화: 계산 복잡도 = O(T²)
토큰 개수의 제곱에 비례해서 계산량이 증가합니다.
실제 문제
PDF를 요약해달라고 했을 때:
- 10페이지: ✓ 잘 작동
- 100페이지: ✗ 실패
- 뒤쪽 부분 거의 무시
- 이상한 응답
- 계산량 폭발
토큰이 많아지면 행렬이 기하급수적으로 커지고, 메모리와 계산 시간이 감당할 수 없는 수준이 됩니다.
Attention이란?
본질: "어떤 단어가 어떤 단어를 얼마나 긴밀하게 바라보는가"
"I am Sam"
I → am: 0.8 (높은 attention)
I → Sam: 0.3
am → Sam: 0.9
각 단어 쌍의 연관도를 숫자로 나타내는 겁니다.
문제: 모든 토큰이 모든 토큰과 내적 계산을 해야 합니다. N개 토큰이면 N×N번 계산해야 하죠.
RNN의 대안적 장점
RNN에는 Attention Mechanism이 없습니다!
계산 복잡도 비교:
- RNN: O(T) - 선형
- Transformer: O(T²) - 제곱
토큰이 많아져도 RNN은 선형적으로만 증가합니다.
장점: 계산량이 폭발하지 않음
단점: 정보 희석, 장기 의존성 약함
맘바(Mamba): RNN의 부활
최근 나온 맘바(Mamba) 모델이 흥미롭습니다.
핵심 아이디어: RNN + LSTM 결합
혁신: 고정된 W 대신 입력에 따라 W를 적응적으로 변경
기존 RNN: W가 고정 맘바: W가 입력에 반응해서 변함
결과:
- 계산 복잡도: 선형 유지
- Attention 없이도 장기 의존성 캡처
- Transformer의 계산 문제 완화 가능성
완전히 사라진 줄 알았던 RNN이 맘바로 다시 주목받고 있습니다.
Bag of Words는 여전히 쓸모있을까?
원핫 인코딩: 완전히 사장
다 임베딩으로 바뀌었습니다. 단어 임베딩을 안 쓰는 경우는 존재하지 않습니다.
Bag of Words: 특정 상황에서 유용
하지만 Bag of Words는 여전히 쓸 만합니다!
적합한 경우: 순서가 그렇게 중요하지 않을 때
토픽 모델링 예시:
문제: 이 논문이 어떤 분야?
- 컴퓨터 과학?
- 생물학?
- 건축학?
해결:
1. 논문의 단어를 histogram으로 만들기
2. 각 분야의 대표 단어집과 비교
3. 가장 유사한 분야로 분류
문장 순서는 중요하지 않습니다. 어떤 단어가 많이 나왔는지만 알면 되니까요.
역사:
- 과거: 토픽 모델링이 중요한 연구 분야였음
- 현재: 거의 연구 안 되지만, 간단한 문서 분류나 검색에는 여전히 유용
마무리: 세 가지 핵심을 기억하라
RNN은 완벽하지 않았습니다. 정보 희석, gradient vanishing, 병렬 처리 불가... 많은 문제가 있었죠.
하지만 순환 엣지 하나의 아이디어로 순차 데이터 처리의 가능성을 열었다는 점에서 획기적이었습니다.
진화의 역사:
RNN → LSTM → GRU → Transformer → Mamba
Transformer가 현재를 지배하지만, 맘바처럼 RNN의 아이디어를 재해석하는 모델들이 계속 나오고 있습니다.
변하지 않는 핵심 원칙:
- 순서는 중요하다: 섞으면 의미가 망가진다
- 길이는 가변적이다: 모든 길이를 수용해야 한다
- 맥락이 핵심이다: 시간적 연결을 캡처해야 한다
이 세 가지를 어떻게 효율적으로 구현하느냐. 그게 순차 데이터 처리의 영원한 과제입니다.