선형 인자 모델: PCA와 ICA
복습: 인코딩과 디코딩
지난 시간에 인코더-디코더를 배웠습니다. 인코딩은 원래 공간을 은닉 공간으로 변환하는 것이고, 디코딩은 은닉 공간을 다시 원래 공간으로 복원하는 겁니다.
오늘은 이 인코딩과 디코딩을 선형 변환으로 수행하는 방법을 배웁니다. 이걸 **선형 인자 모델(Linear Factor Model)**이라고 부릅니다.
선형 인자 모델이란
X가 Z가 될 때 가중치 행렬 W를 곱해서 변환합니다:
Z = W^T X + α
여기서 α는 bias 역할을 합니다. 이 구조는 사실 우리가 이미 잘 아는 **완전연결층(fully connected layer)**과 100% 동일합니다. 단지 activation 함수가 없을 뿐이죠.
α의 역할은 두 가지입니다:
- 평균 조정: 데이터를 원점으로 옮기기
- 잡음 추가: α를 정규분포로 모델링하면 stochastic한 변환이 됨
α를 생략하면 X와 Z는 결정론적(deterministic) 1대1 매핑이 됩니다. 같은 X를 넣으면 항상 같은 Z가 나오죠. α를 정규분포로 설정하면 같은 X를 넣어도 매번 다른 Z가 나옵니다. 이게 Probabilistic PCA의 아이디어예요.
PCA: 주성분 분석
오늘 배울 **주성분 분석(Principal Component Analysis, PCA)**에서는 α를 없앱니다. 대신 X를 먼저 전처리해서 평균이 0이 되도록 만들어요. 그러면 변환식이 간단해집니다:
Z = W^T X
W^T 행렬을 자세히 보면 Q개의 벡터 u₁, u₂, ..., u_Q로 구성되어 있습니다:
W^T = [u₁^T]
[u₂^T]
[...]
[u_Q^T]
각각의 u는 X를 Z로 projection하는 벡터입니다. 내적을 통해서 D차원을 Q차원으로 매핑하는 거죠. 결국 퍼셉트론 여러 개를 쌓은 것과 같습니다.
PCA의 목적: 특별한 U 찾기
여기까지는 어떤 선형 모델이든 똑같습니다. PCA의 핵심은 특별한 U를 찾는 것입니다.
예를 들어 u = [1, 0]이면? X의 x축 정보만 남고 y축 정보는 사라집니다.
u = [0, 1]이면? y축만 남고 x축은 제거됩니다.
u = [√2/2, √2/2]이면? y = x 방향, 즉 대각선 축으로 projection됩니다.
PCA는 이런 여러 가지 가능한 U 중에서 가장 바람직한 U를 찾는 겁니다.
무엇이 바람직한가?
점이 4개 있다고 해봅시다. x축으로 projection하면 두 점이 같은 곳에 겹쳐버립니다. 원래 4개였던 점이 2개로 줄어요. 정보가 손실된 거죠.
projection된 공간에서 다시 원래 점을 복원하라고 하면? 이미 같은 곳에 맵핑된 점들은 구분할 수가 없습니다. 환원 불가능해요.
반면 대각선 축으로 projection하면? 4개 점이 각각 다른 위치에 맵핑됩니다. 정보가 보존된 거죠.
PCA는 정보 손실을 최소화하는 축을 찾습니다. 다시 말해, projection된 Z축에서 점들이 최대한 퍼져있는 축을 찾는 거예요.
정보량 = 분산
점들이 퍼져있다는 건 분산이 크다는 뜻입니다.
두 점이 한 점으로 모여버리면 분별이 안 되죠. 반대로 점들이 산포되어 있으면 구분이 쉽습니다. 따라서:
Z축에서의 분산이 클수록 정보 손실이 적다.
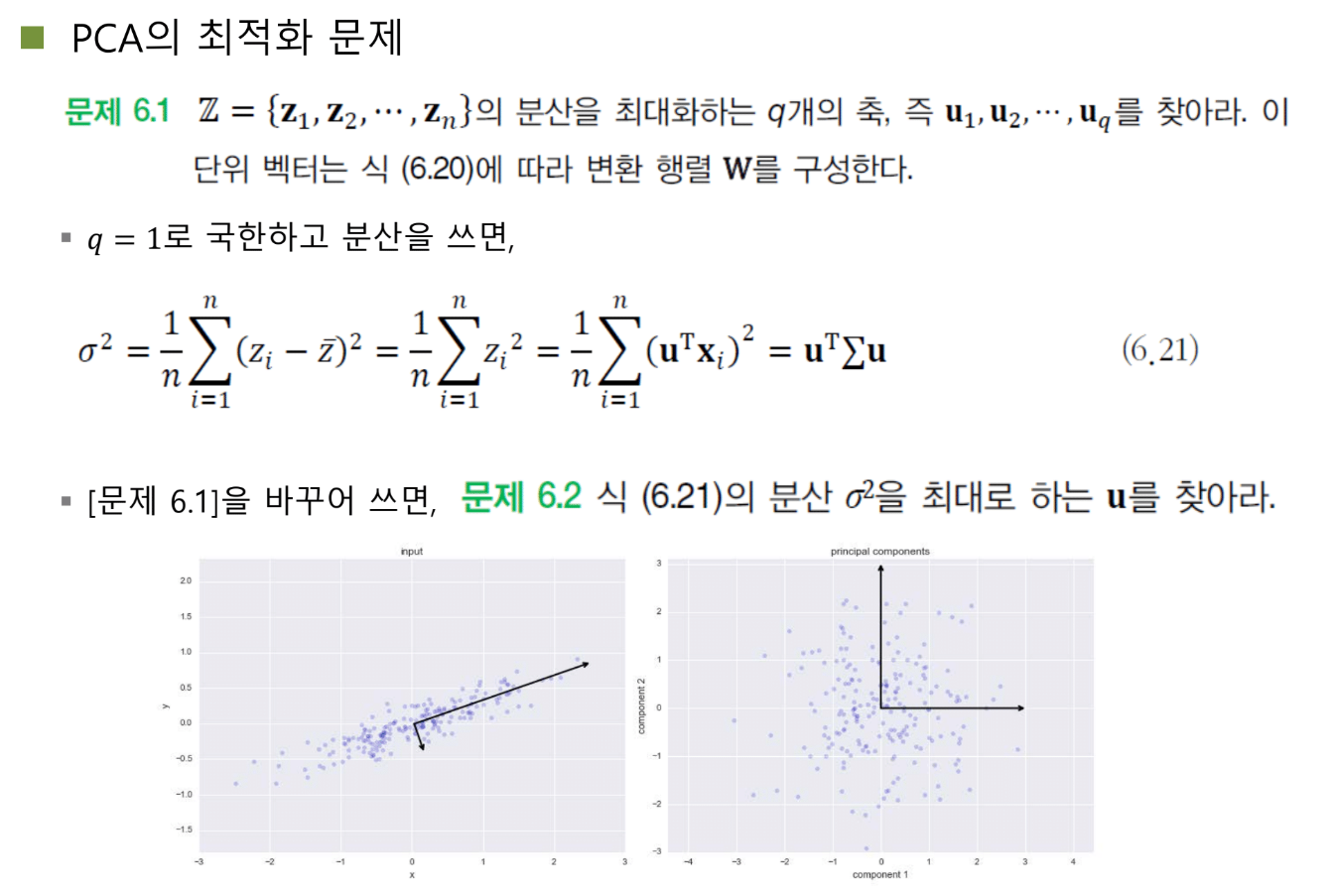
PCA의 목적은 분산을 최대화하는 축을 찾는 것입니다.

최적화 문제로 정리
Z의 분산을 최대화하는 Q개의 축을 찾으시오.
Q=1로 단순화하면, 가장 정보량이 많은 축 하나를 찾는 문제가 됩니다.
분산을 수식으로 쓰면:
Var(Z) = E[(Z - E[Z])²]
X가 이미 평균 0이고 U가 orthonormal(정규직교)하면 Z의 평균도 0이 됩니다. 따라서:
Var(Z) = E[Z²] = E[(U^T X)²] = U^T E[XX^T] U = U^T Σ U
여기서 Σ = E[XX^T]는 공분산 행렬입니다. 각 특징들의 분산과 두 특징 간의 상관관계 정보를 담고 있죠.
공분산 행렬은 X로부터 결정되는 상수입니다. 우리가 바꿀 수 없어요. 결국 U를 잘 조절해서 U^T Σ U를 최대화하면 됩니다.
제약 조건
U는 단위벡터여야 합니다. U^T U = 1이라는 조건이 있어요.
왜냐하면 U의 크기를 무한히 키우면 분산도 무한히 커지기 때문이죠. 의미 있는 최적화를 위해 U의 크기를 1로 고정합니다.
이제 문제가 됩니다:
maximize U^T Σ U
subject to U^T U = 1
조건부 최적화 문제죠.
라그랑주 승수법
조건이 있을 때 최적화하는 좋은 방법이 **라그랑주 승수법(Lagrange Multiplier)**입니다.
핵심 원리
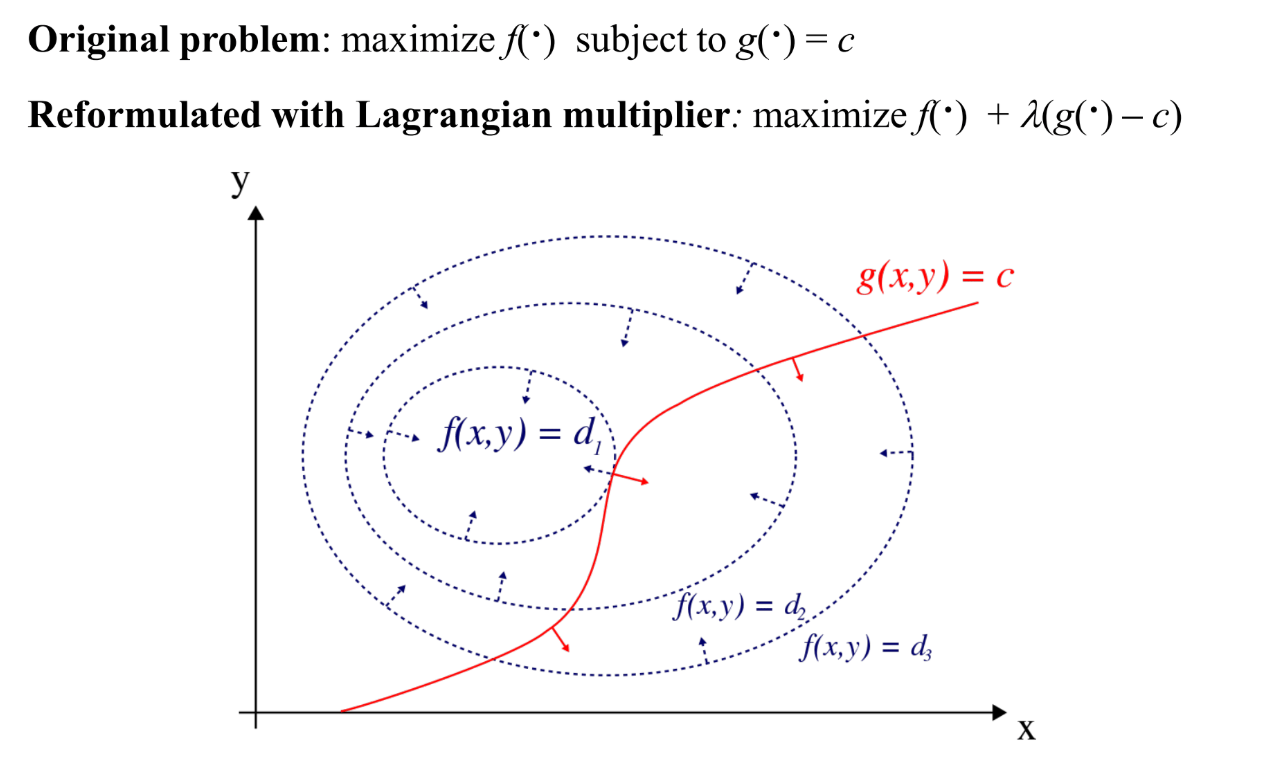
라그랑주가 발견한 사실이 있습니다: 조건부 최적화 문제에서 해가 발생하는 지점에서는 목적함수 F의 gradient와 조건함수 G의 gradient가 평행하다.
∇F = λ∇G
λ는 양수일 수도 음수일 수도 있지만, 어쨌든 두 gradient가 같은 방향 또는 정반대 방향이라는 거예요.
이걸 적분하면 라그랑주 승수법의 공식이 나옵니다:
L = F(x) + λ(G(x) - c)
원래 목적함수에 λ × 조건식을 더해서 하나의 수식으로 만든 거죠.
익숙한 형태
사실 우리는 이미 라그랑주 승수법을 써왔습니다. 딥러닝에서 regularization 기억나시죠?
Loss = MSE + λ||W||²
이건 "MSE를 최소화하는데, W가 가급적 0이었으면 좋겠다"는 조건을 라그랑주 승수법으로 표현한 겁니다. 모든 게 연결되어 있어요.
PCA에 적용
PCA 문제를 라그랑주 승수법으로 다시 쓰면:
L = U^T Σ U - λ(U^T U - 1)
U로 미분해서 0으로 놓으면:
2ΣU - 2λU = 0
ΣU = λU
이 식 어디서 본 적 있지 않나요?
고유값 분해와의 연결
바로 **고유값 분해(Eigenvalue Decomposition)**입니다!
ΣU = λU
선형 시스템 Σ에 벡터 U를 입력으로 넣으면, 같은 방향으로 λ배 스케일링된 벡터가 나옵니다. 이때의 λ를 고유값, U를 고유벡터라고 부르죠.
놀라운 발견: PCA로 분산 최대화하는 축을 찾아봤더니, 고유값 분해와 완전히 같더라!
여기서 λ는 분산값입니다. 고유값이 크다는 건 그 축으로 projection했을 때 분산이 크다는 뜻이에요.
모든 건 연결되어 있다
고유값 분해를 배울 때는 "U를 λ배 스케일링하는 거구나" 정도로 이해했을 수 있습니다. 하지만 더 깊은 의미는 분산을 최대화하는 축이었던 거예요.
Cross entropy가 negative log likelihood와 같은 것처럼, 주성분 분석 관점에서 보느냐 행렬 분해 관점에서 보느냐에 따라 말만 다를 뿐 같은 행동을 하고 있습니다.
PCA 알고리즘
- 공분산 행렬 계산: Σ = X^T X
- 고유값/고유벡터 계산: D개의 고유값-고유벡터 쌍을 구함
- 정렬: 고유값이 큰 순서대로 나열 (고유값은 모두 양수로 만들 수 있음)
- 선택: 상위 Q개의 고유벡터만 선택해서 W에 채움
이렇게 하면 D차원을 Q차원으로 축소하는 인코딩 과정이 완성됩니다.
역변환: 디코딩
Z를 다시 X로 변환하려면 W^T의 역행렬을 곱하면 됩니다.
그런데 W가 정규직교행렬이면 W^T의 역행렬이 W와 같습니다. 따라서:
인코딩: Z = W^T X
디코딩: X̂ = W Z
아주 간단하죠.
기하학적 의미
복잡한 최적화를 거쳤지만, 실제로 수행한 일은 뭘까요?
축을 회전시킨 것에 불과합니다.
원래 x축, y축이 있었는데, 분산이 최대화되는 방향으로 축을 재정의한 거예요. 샘플을 분산이 최대화되는 축에 x축이 걸치도록 회전한 것과 같습니다.
PCA는 결국 회전 행렬을 곱한 것입니다. W가 회전이면 W^T는 역회전이니까, 원래대로 복원이 되는 거죠.

정보 손실에 대한 질문
학생이 질문했습니다: "N차원을 N차원으로 보내면 정보 손실이 0인가요?"
네, W가 정규직교행렬이면 정보 손실 0입니다. 단순히 축을 회전한 것뿐이니까요.
PCA의 응용
데이터 압축
실제로는 D보다 Q가 압도적으로 작습니다. 1000차원을 10차원으로 줄여도 정보량이 상당히 유지돼요.
유튜브 스트리밍을 생각해보세요. 여러분이 스마트폰에서 받는 건 사실 압축된 Z입니다. 디코더로 X(이미지)로 복원하는 거죠.
시각화
Q를 2나 3으로 하면 시각화가 가능합니다. 그냥 막 차원 축소한 게 아니라, 가장 중요한 축에 대해서 시각화하는 거예요.
건물을 봤을 때 자잘한 방이나 가구가 아니라, 건물의 기둥과 구조 - 전체 모양을 좌우하는 큰 프레임을 보는 것과 같습니다.
Eigenface: 얼굴 인식
얼굴 영상을 저차원(예: 7차원)으로 변환합니다. 얼굴의 디테일은 날아가고 주 골격만 남아요.
철수와 영희를 가장 잘 구분할 수 있는 핵심 특징만 남는 거죠. 새로운 얼굴이 들어오면 같은 방식으로 저차원에 매핑하고, 거리가 가장 가까운 사람으로 분류합니다.
평균 얼굴
많은 얼굴로 PCA를 수행하고, 저차원 공간에서 클러스터링해서 중심에 가까운 이미지들을 합성하면 대표 얼굴이 나옵니다.
중국, 일본, 한국, 태국, 브라질, 몽골 등 각 나라의 "평균 얼굴"을 만들 수 있어요. Z 공간의 평균에 수렴하는 얼굴들이죠.

차원 축소의 엄청난 장점
차원 축소를 잘하면 계산량을 무지하게 줄일 수 있습니다.
Search space가 100차원이라 도저히 못 찾겠으면? 3차원으로 줄인 다음 거기서 찾으면 훨씬 빨라요.
축 해석의 한계
학생이 질문했습니다: "PCA 축을 해석할 수 있나요?"
키와 몸무게가 있으면, PCA 축은 "0.5×키 + 0.4×몸무게" 같은 선형 결합이 됩니다. 물리적 해석은 불가능해요.
단지 "이 축이 중요한 축이다, 중요한 특징이다"라고 추상적으로 이해할 뿐, "이건 키다, 몸무게다" 하고 해석할 수는 없습니다.
차원 축소와 매니폴드
학생이 좋은 질문을 했습니다: "차원 축소하면 매니폴드도 작아지나요?"
ChatGPT에 물어보니, 대부분 경우 줄어든다고 합니다. 분산이 큰 방향만 남기고 작은 방향을 제거하기 때문이에요.
하지만 매니폴드의 본질은 유지됩니다. 그리고 X 공간과 Z 공간에서의 augmentation은 근본적으로 다릅니다:
- X 공간: 이미지 회전, 밝기 조절 등 물리적 변형
- Z 공간: 가우시안 노이즈 추가, 보간 등 통계적 변형
Z 공간에서는 매니폴드 구조에 맞춰서 이동하기 쉽고, 매니폴드 근접 유지가 용이합니다.

ICA: 독립 성분 분석
두 번째 선형 인자 모델은 **독립 성분 분석(Independent Component Analysis, ICA)**입니다.
블라인드 원음 분리 문제
미슐랭 3성급 레스토랑에 갔습니다. 스테이지에서 한 명은 바이올린을 켜고, 한 명은 노래를 부르고 있어요.
여러분과 친구가 앉은 위치가 다릅니다. 친구는 바이올린과 가깝고 가수와 멀어요. 여러분은 반대죠. 거리에 따라 듣는 신호가 조금 달라집니다.
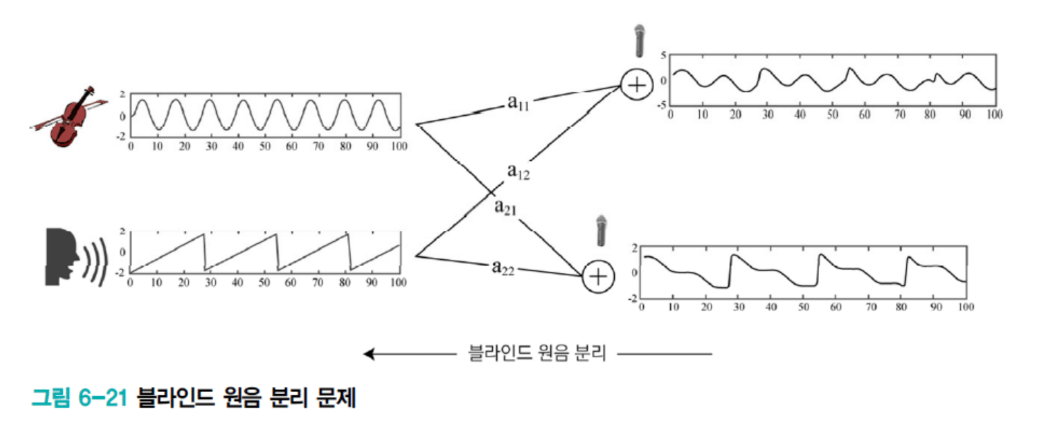
블라인드 원음 분리: 두 개의 관측 포인트로부터 원래 두 개의 음원을 복원하는 문제입니다.
이게 가장 많이 쓰이는 곳이 보이스톡/페이스톡입니다. 카페에서 통화할 때 뒤에서 떠드는 소리, 배경음악 등이 섞이지만 블라인드 원음 분리가 잘 되기 때문에 여러분 목소리만 키워주고 배경음은 줄여줍니다.
수학적 정의
원래 신호를 Z₁, Z₂라고 하고, 관측된 신호를 X₁, X₂라고 합시다.
X₁ = a₁₁Z₁ + a₁₂Z₂
X₂ = a₂₁Z₁ + a₂₂Z₂
행렬로 쓰면:
X = AZ
A를 구할 수 있으면 A의 역행렬로 원음 Z를 복원할 수 있습니다.
Ill-posed 문제
문제는 이게 ill-posed 문제라는 겁니다. 관측한 것보다 예측해야 하는 파라미터가 더 많아요.
32를 주고 "어떤 두 수의 곱인지 맞춰봐"라고 하면? 정답이 무수히 많죠. 이런 문제를 풀려면 추가 조건이 필요합니다.
독립성과 비가우시안
ICA에서 주는 조건은 두 가지입니다:
- 독립성: Z₁과 Z₂는 서로 독립적으로 발생
- 비가우시안: Z의 분포가 가우시안이 아님
독립성은 바이올린과 가수가 내는 소리가 서로 영향을 주지 않는다는 뜻입니다. 각각 따로 생성된 신호죠.
비가우시안이 왜 필요할까요? 가우시안 + 가우시안 = 가우시안이기 때문입니다. 두 가우시안 신호가 섞이면 분리가 불가능해요. 실제 음원은 비가우시안 특성을 가지고 있어서 이 조건을 사용할 수 있습니다.

첨도(Kurtosis)
비가우시안을 측정하는 방법이 첨도입니다. 통계적으로 4차 모멘트에 해당해요.
- 1차 모멘트: 평균
- 2차 모멘트: 분산
- 3차 모멘트: 왜도(skewness)
- 4차 모멘트: 첨도(kurtosis)
첨도는 분포가 얼마나 뾰족한지를 나타냅니다:
- 첨도 = 0: 가우시안
- 첨도 > 0: 가우시안보다 뾰족함
- 첨도 < 0: 가우시안보다 평평함
사람의 목소리를 샘플링해서 분포를 그려보면, 중간 음역에서 대부분의 샘플이 발생합니다. 뾰족한 분포가 되죠. 바이올린도 마찬가지입니다.
ICA 알고리즘
- 평균이 0이 되도록 전처리
- 상관관계(correlation)를 제거 (PCA로 가능)
- 첨도를 최대화하는 A를 찾음
첨도가 최대화되도록 복원하면, 각 원음의 뾰족한 분포가 살아나면서 분리가 잘 됩니다.
PCA vs ICA
PCA ICA
| 가정 | 가우시안 | 비가우시안 |
| 측정 | 2차 모멘트 (분산) | 4차 모멘트 (첨도) |
| 축 관계 | 직교 (orthonormal) | 비직교 가능 |
| 용도 | 차원 축소 | 원음 분리 |
PCA는 분산을 쓴다는 것 자체가 가우시안을 가정한 거예요. ICA는 비가우시안을 가정하고 첨도를 씁니다.
PCA의 축들은 반드시 서로 수직입니다. ICA는 그런 제약이 없어서 자유도가 더 높아요.
ICA의 발명자
ICA를 처음 발명한 분이 **한국인(재미교포)**입니다. 원음 분리를 너무 잘해서 퀄컴에서 특허와 회사를 인수하고, 그분을 부사장으로 앉혔어요.
복습 질문
1. PCA의 목적과 최적화 문제
목적: 정보를 가장 많이 보존하면서 데이터를 저차원으로 변환
정보 측정 방법: 분산. Z축에서의 분산이 클수록 정보 손실이 적음
최적화 문제:
maximize U^T Σ U
subject to U^T U = 1
라그랑주 승수법을 적용하면:
ΣU = λU
고유값 분해 문제가 됨. λ(고유값) = 분산값
2. 라그랑주 승수법은 언제 사용하는가?
어떤 함수를 최적화하고 싶은데 등식 조건이 있을 때 사용합니다.
핵심 원리: 해가 발생하는 지점에서 목적함수 F의 gradient와 조건함수 G의 gradient가 평행합니다.
∇F = λ∇G
이걸 하나의 식으로 합치면:
L = F(x) + λ(G(x) - c)딥러닝의 regularization도 같은 원리입니다:
Loss = MSE + λ||W||²
"MSE 최소화" + "W가 0에 가깝게" 조건
3. PCA와 고유값 분해의 관계
PCA로 분산을 최대화하는 축을 찾으면, 고유값 분해 문제가 됩니다:
ΣU = λU
- U(고유벡터) = 주성분 축
- λ(고유값) = 그 축에서의 분산값
고유값이 큰 순서대로 나열하면, 가장 정보량이 많은 축부터 정렬됩니다. 상위 Q개만 선택하면 차원 축소 완료.
결론: 주성분 분석과 행렬 분해는 관점만 다를 뿐 같은 것
4. PCA의 기하학적 의미
PCA는 축을 회전시킨 것에 불과합니다.
원래 x축, y축을 분산이 최대화되는 방향으로 재정의한 거예요. W가 정규직교행렬이므로 회전 행렬입니다.
- 인코딩: Z = W^T X (회전)
- 디코딩: X̂ = W Z (역회전)
N차원을 N차원으로 보내면 정보 손실 0. 단순히 회전만 한 거니까요.
5. ICA가 필요한 이유와 작동 원리
필요한 이유: 블라인드 원음 분리. 섞인 신호에서 원래 신호를 복원
문제: X = AZ에서 A를 찾는 것은 ill-posed (해가 무수히 많음)
추가 조건:
- 독립성: Z₁, Z₂가 서로 독립적으로 발생
- 비가우시안: 분포가 뾰족함 (첨도 사용)
원리: 첨도를 최대화하는 A를 찾음. 원음의 뾰족한 분포가 복원되면서 분리 성공
PCA와 차이:
- PCA: 가우시안 가정, 2차 모멘트(분산), 직교 축
- ICA: 비가우시안 가정, 4차 모멘트(첨도), 비직교 가능